题目内容
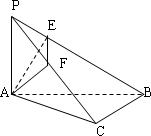
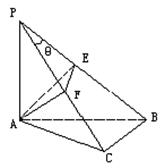
如图,在斜边为AB的Rt△ABC中,过点A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.

(1)求证:BC⊥平面PAC.
(2)求证:PB⊥平面AMN.
答案:
解析:
解析:
证明:(1)∵△ABC是直角三角形,
∴BC⊥AC.
∵PA⊥平面ABC,
∴PA⊥BC.
∴BC⊥平面PAC.
(2)由(1)知BC⊥平面PAC,
∴BC⊥AN.
又∵AN⊥PC,
∴AN⊥平面PBC,
∴AN⊥PB.
又∵PB⊥AM,BM∩AN=A,
∴PB⊥平面AMN.
思路分析:证明直线和平面内的两条相交直线垂直.(1)由题易知BC⊥AC,BC⊥PA,结论成立.
(2)AN⊥BC,AN⊥PC,结论成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

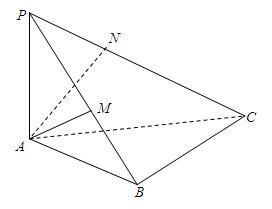 21、如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.
21、如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.