题目内容
当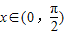
时，函数
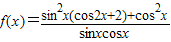的最小值是 ．
【答案】分析：由于函数的形式较复杂，不易判断最值在何处取到，故可先由三角函数公式对函数解析式进行化简，再根据化简后的形式判断其最值，由于函数最终化简为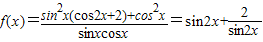
，观察知，此函数不适合用基本不等式，故可令t=sin2x，将函数变为
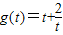，由单调性求最值即可．
解答：解：由题意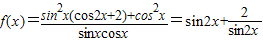
令t=sin2x，则函数可变为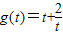
，由于
，可得2x∈（0，π），即t=sin2x∈[0，1]
由于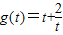
在[0，1]上是减函数，故其最小值为1+2=3
所以当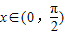
时，函数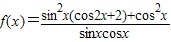
的最小值是3
故答案为3
点评：本题考查求函数的最值，解题的关键是将函数解析式化简再由换元法将求三角函数的最值问题转化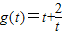
在[0，1]上的最值问题，本题用到了换元法的技巧，在求解较复杂的函数的最值问题时常用换元法将函数形式化简，以方便求解
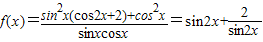，观察知，此函数不适合用基本不等式，故可令t=sin2x，将函数变为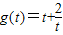，由单调性求最值即可．解答：解：由题意
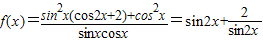
令t=sin2x，则函数可变为
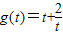，由于，可得2x∈（0，π），即t=sin2x∈[0，1]由于
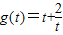在[0，1]上是减函数，故其最小值为1+2=3所以当
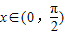时，函数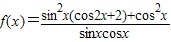的最小值是3故答案为3
点评：本题考查求函数的最值，解题的关键是将函数解析式化简再由换元法将求三角函数的最值问题转化
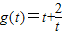在[0，1]上的最值问题，本题用到了换元法的技巧，在求解较复杂的函数的最值问题时常用换元法将函数形式化简，以方便求解 
练习册系列答案
相关题目
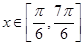时，函数
的最小值是_______，最大值是________。
时，函数
的最小值是_______，最大值是________。
时，函数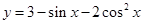
的最小值是_______，最大值是________。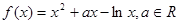
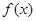在[1,2]上是减函数,求实数
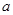的取值范围；
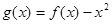，是否存在实数
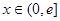时，函数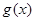
的最小值是3，若存在，求出