题目内容
设函数,f(x)=sin(2ωx+φ)在(ω>0,-π<φ<0],函数y=f(x)的相邻两条对称轴间距离为π,且函数的图象的一个对称中心为(-| π |
| 2 |
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)在△ABC中,若f(A)=-
2
| ||
| 5 |
3
| ||
| 10 |
分析:(Ⅰ)函数y=f(x)的相邻两条对称轴间距离为π,求出函数周期,得到ω,函数的图象的一个对称中心为(-
,0).求出φ,然后求出函数y=f(x)的解析式;
(Ⅱ)在△ABC中,通过f(A)=-
,求出cosA,sinA,f(B)=-
,求出cosB,sinB,利用cosC=cos[π-A-B]求出cosC,根据C的范围求角C的大小.
| π |
| 2 |
(Ⅱ)在△ABC中,通过f(A)=-
2
| ||
| 5 |
3
| ||
| 10 |
解答:解:(Ⅰ)∵函数y=f(x)的相邻两条对称轴间距离为π,
∴T=
=2π,ω=
,
又 函数的图象的一个对称中心为(-
,0)
∴sin(-
+φ)=0 而-π<φ<0
∴φ=-
.
所以函数y=f(x)的解析式为y=sin(x-
)=-cosx
(Ⅱ)由(Ⅰ)可知:cosA=
,cosB=
,又A,B∈(0,π),
所以,sinA=
,sinB=
,
cosC=cos[π-A-B]=cos(A+B)=-(cosAcosB-sinAsinB)
=-(
×
-
×
)=-
,
又C∈(0,π),∴C=
.
∴T=
| 2π |
| 2ω |
| 1 |
| 2 |
又 函数的图象的一个对称中心为(-
| π |
| 2 |
∴sin(-
| π |
| 2 |
∴φ=-
| π |
| 2 |
所以函数y=f(x)的解析式为y=sin(x-
| π |
| 2 |
(Ⅱ)由(Ⅰ)可知:cosA=
2
| ||
| 5 |
3
| ||
| 10 |
所以,sinA=
| ||
| 5 |
| ||
| 10 |
cosC=cos[π-A-B]=cos(A+B)=-(cosAcosB-sinAsinB)
=-(
2
| ||
| 5 |
3
| ||
| 10 |
| ||
| 5 |
| ||
| 10 |
| ||
| 2 |
又C∈(0,π),∴C=
| 3π |
| 4 |
点评:本题是基础题,考查三角函数的解析式的求法,注意周期的应用,两角和的余弦公式的应用,同时注意C的范围,以及角的变换的技巧,是解题的关键,考查计算能力.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目

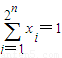 ,证明:
,证明: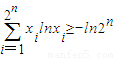
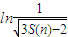 (i,n∈N*).
(i,n∈N*).