题目内容
已知某企业原有员工2000人,每人每年可为企业创利3.5万元.为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的5%,并且每年给每位待岗员工发放生活补贴0.5万元.据评估,当待岗员工人数x不超过原有员工1%时,留岗员工每人每年可为企业多创利(1-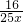 )万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利0.9万元.为使企业年利润最大,应安排多少员工待岗?
)万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利0.9万元.为使企业年利润最大,应安排多少员工待岗?
解:设重组后,该企业年利润为y万元.
当待岗人员不超过1%时,由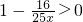 ,x≤2000×1%=20,得0<x≤20(x∈N),
,x≤2000×1%=20,得0<x≤20(x∈N),
则y=(2000-x)(3.5+1-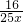 )-0.5x=-5(x+
)-0.5x=-5(x+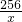 )+9000.64;(3分)
)+9000.64;(3分)
当待岗人员超过1%且不超过5%时,由20<x≤2000×5%,得20<x≤100(x∈N),
则y=(2000-x)(3.5+0.9)-0.5x=-4.9x+8800.(6分)
∴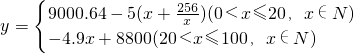 (7分)
(7分)
当0<x≤20且x∈N时,有
y=-5(x+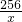 )+9000.64≤-5×
)+9000.64≤-5×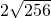 +9000.64=8840.64,
+9000.64=8840.64,
当且仅当x=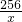 ,即x=16时取等号,此时y取得最大值,最大值是8840.64;(9分)
,即x=16时取等号,此时y取得最大值,最大值是8840.64;(9分)
当20<x≤100且x∈N时,函数y=-4.9x+8800为减函数.
所以y<-4.9×20+8800=8702.(11分)
综上所述,当x=16时,y有最大值8840.64万元.
即要使企业年利润最大,应安排16名员工待岗.(12分)
分析:利用在岗员工人数乘以留岗员工每人每年可为企业多创利;分两段求出企业年利润,得到的是分段函数;利用基本不等式求出第一段函数的最大值;再利用一次函数的单调性求出第二段函数的最小值,从两个最小值中比较出最小值.
点评:本题考查将实际问题转化为数学问题的能力、考查求分段函数的最值时分段求再挑出最值中的最值、考查利用基本不等式求函数的最值注意满足的条件:一正、二定、三相等.
当待岗人员不超过1%时,由
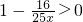 ,x≤2000×1%=20,得0<x≤20(x∈N),
,x≤2000×1%=20,得0<x≤20(x∈N),则y=(2000-x)(3.5+1-
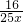 )-0.5x=-5(x+
)-0.5x=-5(x+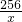 )+9000.64;(3分)
)+9000.64;(3分)当待岗人员超过1%且不超过5%时,由20<x≤2000×5%,得20<x≤100(x∈N),
则y=(2000-x)(3.5+0.9)-0.5x=-4.9x+8800.(6分)
∴
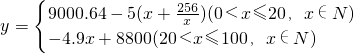 (7分)
(7分)当0<x≤20且x∈N时,有
y=-5(x+
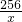 )+9000.64≤-5×
)+9000.64≤-5×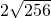 +9000.64=8840.64,
+9000.64=8840.64,当且仅当x=
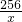 ,即x=16时取等号,此时y取得最大值,最大值是8840.64;(9分)
,即x=16时取等号,此时y取得最大值,最大值是8840.64;(9分)当20<x≤100且x∈N时,函数y=-4.9x+8800为减函数.
所以y<-4.9×20+8800=8702.(11分)
综上所述,当x=16时,y有最大值8840.64万元.
即要使企业年利润最大,应安排16名员工待岗.(12分)
分析:利用在岗员工人数乘以留岗员工每人每年可为企业多创利;分两段求出企业年利润,得到的是分段函数;利用基本不等式求出第一段函数的最大值;再利用一次函数的单调性求出第二段函数的最小值,从两个最小值中比较出最小值.
点评:本题考查将实际问题转化为数学问题的能力、考查求分段函数的最值时分段求再挑出最值中的最值、考查利用基本不等式求函数的最值注意满足的条件:一正、二定、三相等.

练习册系列答案
相关题目
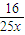 )万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利0.9万元.为使企业年利润最大,应安排多少员工待岗?
)万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利0.9万元.为使企业年利润最大,应安排多少员工待岗?