题目内容
已知| OA |
| a |
| OB |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
分析:根据所给的条件可以看出三角形是一个等边三角形,则各边之间的关系就很清楚,根据平行四边形法则和三角形法则看出两个向量的和和差对应的向量,得到夹角,利用正弦定理得到三角形的面积.
解答:解:∵知
=
,
=
,且|
|=|
|=4,∠AOB=60°,
∴三角形OAB是一个正三角形,
+
在角O的平分线上,
∴
+
与
的夹角是30°,
-
与
的夹角是60°,
△AOB的面积是
×4×4×sin60°=4
故答案为:30°;60°;4
.
| OA |
| a |
| OB |
| b |
| a |
| b |
∴三角形OAB是一个正三角形,
| a |
| b |
∴
| a |
| b |
| a |
| a |
| b |
| a |
△AOB的面积是
| 1 |
| 2 |
| 3 |
故答案为:30°;60°;4
| 3 |
点评:本题考查向量的平行四边形法则,考查三角形法则,考查向量的夹角和正弦定理,是一个综合题,解题时可以做出图象利于观察.

练习册系列答案
相关题目
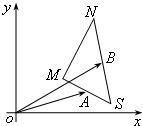 如图,已知
如图,已知