题目内容
5.a,b,c分别表示三条直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;②若b?M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥b,a⊥M,则b∥M;⑤若a?M,b∥M,a∥b,则a∥M其中正确命题的有⑤(只填序号)
分析 在①中,a与b相交、平行或异面;在②中,a∥M或a?M;在③中,a与b相交、平行或异面;在④中,b∥M或b?M;在⑤中,由线面平行的判定定理得a∥M.
解答 解:由a,b,c分别表示三条直线,M表示平面,知:
在①中:若a∥M,b∥M,则a与b相交、平行或异面,故①错误;
在②中:若b?M,a∥b,则a∥M或a?M,故②错误;
在③中:若a⊥c,b⊥c,则a与b相交、平行或异面,故③错误;
在④中:若a⊥b,a⊥M,则b∥M或b?M,故④错误;
在⑤中:若a?M,b∥M,a∥b,则由线面平行的判定定理得a∥M,故⑤正确.
故答案为:⑤.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
16.抛物线x=2ay2的准线方程是x=1,则a的值是( )
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | -2 | D. | 2 |
13.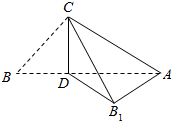 如图所示,将直角三角形ABC以斜边AB上的高CD为棱折成一个三棱锥C一ADB1,且使得平面ACD⊥平面B1CD,记BC=a,AC=b(a,b为变量),则∠B1CA的最小值为( )
如图所示,将直角三角形ABC以斜边AB上的高CD为棱折成一个三棱锥C一ADB1,且使得平面ACD⊥平面B1CD,记BC=a,AC=b(a,b为变量),则∠B1CA的最小值为( )
 如图所示,将直角三角形ABC以斜边AB上的高CD为棱折成一个三棱锥C一ADB1,且使得平面ACD⊥平面B1CD,记BC=a,AC=b(a,b为变量),则∠B1CA的最小值为( )
如图所示,将直角三角形ABC以斜边AB上的高CD为棱折成一个三棱锥C一ADB1,且使得平面ACD⊥平面B1CD,记BC=a,AC=b(a,b为变量),则∠B1CA的最小值为( )| A. | 45° | B. | 60° | C. | 75° | D. | 30° |
20.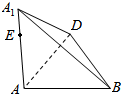 如图,在三棱锥A1-ABC中,A1A=AB=AD=2,A1A⊥平面ABD,∠DAB=90°,AE=$\frac{4}{3}$,动点F在△A1BD(包括边界)上运动,则AF+EF的最小值为( )
如图,在三棱锥A1-ABC中,A1A=AB=AD=2,A1A⊥平面ABD,∠DAB=90°,AE=$\frac{4}{3}$,动点F在△A1BD(包括边界)上运动,则AF+EF的最小值为( )
 如图,在三棱锥A1-ABC中,A1A=AB=AD=2,A1A⊥平面ABD,∠DAB=90°,AE=$\frac{4}{3}$,动点F在△A1BD(包括边界)上运动,则AF+EF的最小值为( )
如图,在三棱锥A1-ABC中,A1A=AB=AD=2,A1A⊥平面ABD,∠DAB=90°,AE=$\frac{4}{3}$,动点F在△A1BD(包括边界)上运动,则AF+EF的最小值为( )| A. | $\frac{4\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |