题目内容
先阅读第(1)题的解法,再解决第(2)题:(1)已知向量
 ,求x2+y2的最小值.
,求x2+y2的最小值.解:由
 得
得 ,当
,当 时取等号,
时取等号,所以x2+y2的最小值为

(2)已知实数x,y,z满足2x+3y+z=1,则x2+y2+z2的最小值为 .
【答案】分析:构造向量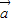 =(2,3,1),
=(2,3,1),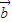 =(x,y,z),类比(1)的解法可得.
=(x,y,z),类比(1)的解法可得.
解答:解:由题意,构造向量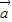 =(2,3,1),
=(2,3,1),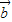 =(x,y,z),
=(x,y,z),
显然有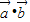 =2x+3y+z=1,
=2x+3y+z=1,
由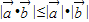 得1≤
得1≤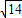
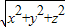 ,
,
解得x2+y2+z2≥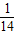 ,当
,当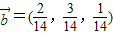 时取等号.
时取等号.
故答案为: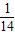
点评:本题考查平面向量数量积的运算,涉及类比的方法,属中档题.
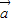 =(2,3,1),
=(2,3,1),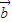 =(x,y,z),类比(1)的解法可得.
=(x,y,z),类比(1)的解法可得.解答:解:由题意,构造向量
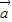 =(2,3,1),
=(2,3,1),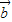 =(x,y,z),
=(x,y,z),显然有
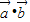 =2x+3y+z=1,
=2x+3y+z=1,由
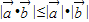 得1≤
得1≤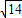
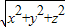 ,
,解得x2+y2+z2≥
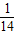 ,当
,当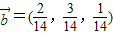 时取等号.
时取等号.故答案为:
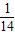
点评:本题考查平面向量数量积的运算,涉及类比的方法,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答:
,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答: )2+
)2+ ,
, 时,u有最大值,umax=
时,u有最大值,umax= ,显然u没有最小值,
,显然u没有最小值, 时,g(x)有最小值4,没有最大值.
时,g(x)有最小值4,没有最大值. ,请提出此问题的一个结论,例如:求通项an.并给出正确解答.
,请提出此问题的一个结论,例如:求通项an.并给出正确解答.