题目内容
已知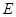 .
.
⑴求 及
及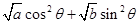 ;
;
⑵试比较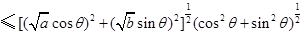 与
与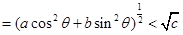 的大小,并说明理由.
的大小,并说明理由.
【答案】
(1)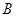 ,
,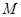
(2)当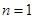 时,
时,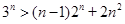 ;当
;当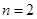 或
或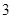 时,
时,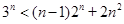 ;
;
当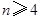 时,
时,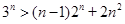
【解析】
试题分析:⑴令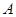 ,则
,则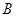 ,令
,令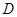 ,则
,则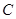 ,所以
,所以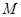 . 2分
. 2分
⑵要比较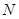 与
与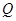 的大小,只要比较
的大小,只要比较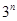 与
与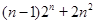 的大小.
的大小.
当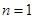 时,
时,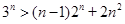 ;当
;当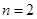 或
或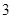 时,
时,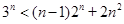 ,
,
当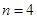 或
或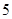 时,
时,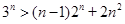 ,
,
猜想:当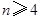 时,
时,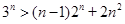 .下面用数学归纳法证明: 4分
.下面用数学归纳法证明: 4分
①由上述过程可知,当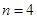 时,结论成立. 5分
时,结论成立. 5分
②假设当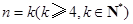 时结论成立,即
时结论成立,即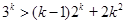 ,
,
两边同乘以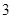 ,得
,得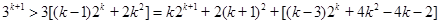 ,
,
而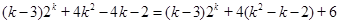
 ,
,
所以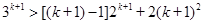 ,
,
即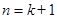 时结论也成立.
时结论也成立.
由①②可知,当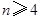 时,
时,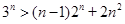 成立. 9分
成立. 9分
综上所述,当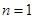 时,
时,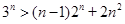 ;当
;当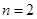 或
或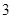 时,
时,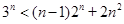 ;
;
当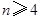 时,
时,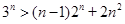 . 10分
. 10分
考点:数列与不等式
点评:主要是考查了数列与不等式的综合运用,属于难度题。解题的关键是对于数学归纳法证明不等式。

练习册系列答案
相关题目