题目内容
(12分) 已知函数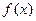 =loga
=loga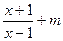 (a>0且a≠1)是奇函数
(a>0且a≠1)是奇函数
(1)求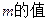 ,(
,(
(2)讨论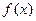 在(1,+∞)上的单调性,并予以证明
在(1,+∞)上的单调性,并予以证明
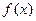 =loga
=loga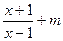 (a>0且a≠1)是奇函数
(a>0且a≠1)是奇函数(1)求
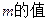 ,(
,((2)讨论
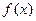 在(1,+∞)上的单调性,并予以证明
在(1,+∞)上的单调性,并予以证明(1)

(2)当a>1时,f(x)=loga
 在(1,+∞)上为减函数;当0<a<1时,f(x)=loga
在(1,+∞)上为减函数;当0<a<1时,f(x)=loga 在(1,+∞)上为增函数
在(1,+∞)上为增函数解:
(1)
(2)设u= ,任取x2>x1>1,则
,任取x2>x1>1,则
u2-u1=
=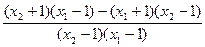
=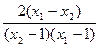 .
.
∵x1>1,x2>1,∴x1-1>0,x2-1>0.
又∵x1<x2,∴x1-x2<0.
∴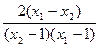 <0,即u2<u1.
<0,即u2<u1.
当a>1时,y=logax是增函数,∴logau2<logau1,
即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,∴logau2>logau1,
即f(x2)>f(x1).
综上可知,当a>1时,f(x)=loga 在(1,+∞)上为减函数;当0<a<1时,f(x)=loga
在(1,+∞)上为减函数;当0<a<1时,f(x)=loga 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.
(1)

(2)设u=
 ,任取x2>x1>1,则
,任取x2>x1>1,则u2-u1=

=
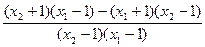
=
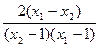 .
.∵x1>1,x2>1,∴x1-1>0,x2-1>0.
又∵x1<x2,∴x1-x2<0.
∴
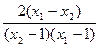 <0,即u2<u1.
<0,即u2<u1.当a>1时,y=logax是增函数,∴logau2<logau1,
即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,∴logau2>logau1,
即f(x2)>f(x1).
综上可知,当a>1时,f(x)=loga
 在(1,+∞)上为减函数;当0<a<1时,f(x)=loga
在(1,+∞)上为减函数;当0<a<1时,f(x)=loga 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
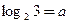 ,
,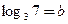 ,试用
,试用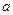 ,
,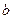 表示
表示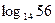 .
. 有最大值1,求实数
有最大值1,求实数 的值.
的值.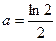 ,
,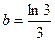 ,
, ,则
,则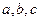 的大小关系为 。
的大小关系为 。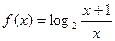
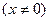 .求
.求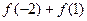 的值.
的值.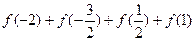 的值.
的值.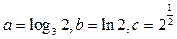 ,则 ( )
,则 ( )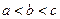
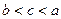
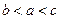
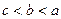
 ,若
,若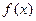 存在零点,则实数
存在零点,则实数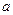 的取值范围( )
的取值范围( )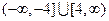

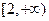

 ,
,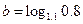 ,
, ,则
,则 、
、 、
、 的大小关系为
的大小关系为 



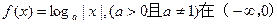 上单调递
上单调递 增,则
增,则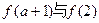 的大小关系为( )
的大小关系为( )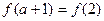 B
B 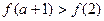 C.
C. 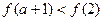 D.不确定
D.不确定