题目内容
球面上有三个点,其中任意两点的球面距离都等于大圆周长的48π
解析:本题考查了球的截面性质、球面距离以及球的表面积公式等知识.设球心为O,半径为R,球面上三点为A、B、C,任两点的球面距离为大圆周长的![]() ,所以可得∠AOB=∠BOC=∠AOC=
,所以可得∠AOB=∠BOC=∠AOC=![]() ,所以有OA=OB=OC=AB=AC=BE,故四面体OABC为正四面体,设过ABC的小圆的半径为r,由4π=2πr,所以r=2.可求得AB=AC=BC=R=2
,所以有OA=OB=OC=AB=AC=BE,故四面体OABC为正四面体,设过ABC的小圆的半径为r,由4π=2πr,所以r=2.可求得AB=AC=BC=R=2![]() .所以表面积S=4πR2=48π.
.所以表面积S=4πR2=48π.

练习册系列答案
相关题目
 的球的球面上有三个点,其中任意两点间的球面距离都等于
的球的球面上有三个点,其中任意两点间的球面距离都等于 ,且经过这三个点的小圆周长为
,且经过这三个点的小圆周长为 ,则
,则
 B.
B. C.
C. D.
D.
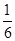 ,经过这3个点的小圆周长为
,经过这3个点的小圆周长为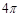 ,那么这个球的半径为(
)
,那么这个球的半径为(
)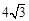 B.
B.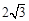 C.
C.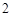 D.
D.