题目内容
△ABC的内角A、B、C的对边分别为a,b,c,asin A+csin C- asin C=bsin B.
asin C=bsin B.
(1)求B;
(2)若A=75°,b=2,求a,c.
 asin C=bsin B.
asin C=bsin B.(1)求B;
(2)若A=75°,b=2,求a,c.
(1) B=45°. (2) a=1+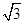 ,c=
,c=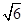 .
.
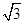 ,c=
,c=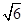 .
.试题分析: (1)由正弦定理得a2+c2-
 ac=b2. (2分)
ac=b2. (2分)由余弦定理得b2=a2+c2-2accos B. (4分)
故cos B=
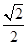 ,又0°<B<180°,因此B=45°. (6分)
,又0°<B<180°,因此B=45°. (6分)(2)sin A=sin(30°+45°)=sin 30°cos 45°+cos 30°sin 45°=
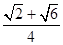 .(8分)
.(8分)故a=b·
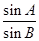 =
=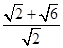 =1+
=1+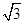 ,(10分)
,(10分)c=b·
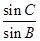 =2·
=2·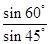 =
=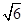 .(12分)
.(12分)点评:典型题,本题解答思路明确,首先应用正弦定理,转化得到边的关系式,利用余弦定理求角。(2)应用正弦定理及两角和与差的三角函数公式,确定边长。本题较易。

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 分别为
分别为 三个内角
三个内角 的对边,
的对边,
 ,
,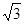 ;求
;求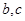 .
.
 m B.50
m B.50 m
m  m
m 中,
中, 分别为内角
分别为内角 所对的边长,
所对的边长, ,
, ,
, ,求:
,求: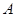 的大小;
的大小; 上的高。
上的高。 中,角
中,角 ,
, ,
, ,的对边分别为
,的对边分别为 .
. ,
,  ,
, .
. 的值;
的值; ,求△
,求△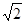 ,那么cosB=( )
,那么cosB=( )



 是极点,则
是极点,则 的面积等于_______;
的面积等于_______;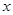 的不等式
的不等式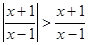 的解集是____ ____。
的解集是____ ____。 ,
, ,
, 。
。 的值;
的值; ,则A等于 .
,则A等于 .