题目内容
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)当![]() 时,若
时,若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() 和
和![]() ,求
,求![]() 的取值范围,并证明:
的取值范围,并证明:![]() .
.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.![]()
【解析】
(1)![]() ,由已知得
,由已知得![]() ,问题转化为
,问题转化为![]() ,
,![]() ,求
,求![]() ,通过判断
,通过判断![]() ,得出
,得出![]() 单调性,以及
单调性,以及![]() ,求出单调区间
,求出单调区间![]() 的极值,最值,进而求出结论;
的极值,最值,进而求出结论;
(2)![]() ,
,![]() ,
,![]() 时,
时,![]() ,至多一个零点,不成立;
,至多一个零点,不成立;![]() 时,求出单调区间,极值,分析
时,求出单调区间,极值,分析![]() 函数值的变化趋势,求得
函数值的变化趋势,求得![]() 由两个零点时,
由两个零点时,![]() ,
,![]() ,设
,设![]() ,并满足
,并满足![]() ,可得
,可得![]() ,令
,令![]() ,则
,则![]() ,即
,即![]() ,要证
,要证![]() ,等价转化为证明
,等价转化为证明![]() ,设
,设![]() ,通过求导,再构造函数再求导,可证
,通过求导,再构造函数再求导,可证![]() 在
在![]() 上单增,即可证明结论.
上单增,即可证明结论.
(1)令![]() ,当
,当![]() 时,
时,![]() .
.
若![]() 对任意
对任意![]() 恒成立,即为
恒成立,即为![]()
∵![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
∴![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
![]() 时,
时,![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() .
.
(2)![]() ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() 在
在![]() 上单增,至多一个零点,不成立;
上单增,至多一个零点,不成立;
![]() 时,由
时,由![]() 得
得![]() ,
,
![]() 在
在![]() 上单减,在
上单减,在![]() 上单增.
上单增.
![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
要存在两零点只需![]() ,即
,即![]() ,得
,得![]() .
.
不妨设![]() ,由
,由![]() 得
得![]() ,
,
令![]() ,则
,则![]() ,即
,即![]() ,而
,而
![]()
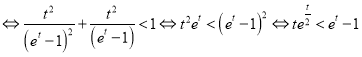 (*)
(*)
令![]() ,
,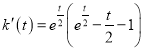 ,
,
令![]() ,
,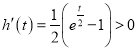 ,
,
∴![]() 在
在![]() 上单增,
上单增,![]() ,
,
∴![]() ,
,![]() 在
在![]() 上单增,
上单增,
![]() ,故(*)成立,得证.
,故(*)成立,得证.

【题目】
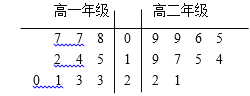
某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀(体育成绩满分100分,不低于85分称优秀)人数之间的关系进行分析研究,他们从本校初二,初三,高一,高二,高三年级各随机抽取了40名学生,记录并整理了这些学生周平均体育锻炼小时数与体育成绩优秀人数,得到如下数据表:
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均体育锻炼小时数工(单位:小时) | 14 | 11 | 13 | 12 | 9 |
体育成绩优秀人数y(单位:人) | 35 | 26 | 32 | 26 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,再用剩下的2组数据进行检验.
(1)若选取的是初三,高一,高二的3组数据,请根据这3组数据,求出y关于x的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?
参考数据:![]() ,
,![]() .
.
参考公式: ,
,![]() .
.
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低