题目内容
证明下列不等式:(1)a,b都是正数,且a+b=1,求证:
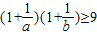 ;
;(2)设实数x,y满足y+x2=0,且0<a<1,求证:
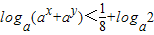 .
.
【答案】分析:(1)由题设知左=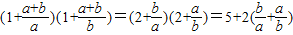 ≥9.
≥9.
(2)由题设知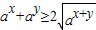 ,由0<a<1,知
,由0<a<1,知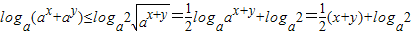 ,由此能够证明
,由此能够证明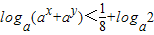 .
.
解答:证明(1)左= (3分)
(3分)
因为a>0,b>0,所以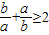 (5分)
(5分)
所以左=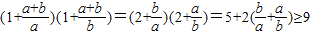 (7分)
(7分)
(2)∵ax>0,ay>0,
∴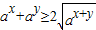 (9分)
(9分)
又∵0<a<1,
∴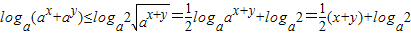 (12分)
(12分)
因为y+x2=0,
∴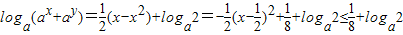
即原不等式得证..(14分)
点评:本题考查不等式的证明,解题时要注意均值不等式的合理运用.
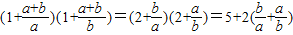 ≥9.
≥9.(2)由题设知
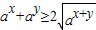 ,由0<a<1,知
,由0<a<1,知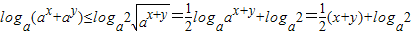 ,由此能够证明
,由此能够证明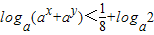 .
.解答:证明(1)左=
 (3分)
(3分)因为a>0,b>0,所以
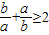 (5分)
(5分)所以左=
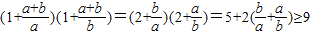 (7分)
(7分)(2)∵ax>0,ay>0,
∴
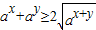 (9分)
(9分)又∵0<a<1,
∴
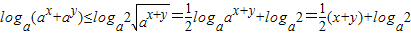 (12分)
(12分)因为y+x2=0,
∴
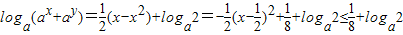
即原不等式得证..(14分)
点评:本题考查不等式的证明,解题时要注意均值不等式的合理运用.

练习册系列答案
相关题目