题目内容
半径为1的球面上的四点A,B,C,D是正四面体的顶点,则A与B两点间的球面距离为( )
A、arccos(-
| ||||
B、arccos(-
| ||||
C、arccos(-
| ||||
D、arccos(-
|
分析:由题意求出正四面体的棱长,利用余弦定理求出∠AOB,然后求出A与B两点间的球面距离.
解答:解:半径为1的球面上的四点A,B,C,D是正四面体的顶点,所以正四面体扩展为正方体的外接球与圆柱球相同,正方体的对角线就是外接球的直径,所以正四面体的棱长为:
;
(
)2=2-2cos∠AOB
cos∠AOB=-
A与B两点间的球面距离为:1×arccos(-
)=arccos(-
)
故选C.
2
| ||
| 3 |
(
2
| ||
| 3 |
cos∠AOB=-
| 1 |
| 3 |
A与B两点间的球面距离为:1×arccos(-
| 1 |
| 3 |
| 1 |
| 3 |
故选C.
点评:本题是基础题,考查正四面体的外接球的知识,考查空间想象能力,计算能力,球面距离的求法,是常考题型.

练习册系列答案
相关题目

 =0,
=0, •
• =0,
=0, •
• =0,用S1、S2、S3分别表示△ABC、△ACD、ABD的面积,则S1+S2+S3的最大值是 .
=0,用S1、S2、S3分别表示△ABC、△ACD、ABD的面积,则S1+S2+S3的最大值是 .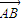
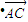 =0,
=0,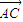 •
•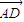 =0,
=0,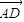 •
•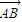 =0,用S1、S2、S3分别表示△ABC、△ACD、ABD的面积,则S1+S2+S3的最大值是 .
=0,用S1、S2、S3分别表示△ABC、△ACD、ABD的面积,则S1+S2+S3的最大值是 .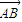
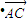 =0,
=0,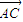 •
•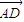 =0,
=0,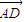 •
•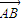 =0,用S1、S2、S3分别表示△ABC、△ACD、ABD的面积,则S1+S2+S3的最大值是 .
=0,用S1、S2、S3分别表示△ABC、△ACD、ABD的面积,则S1+S2+S3的最大值是 .