题目内容
设a、b、c∈R,函数f(x)=x3+ax2+bx+c在x=1和x=3取得极值
(1)求a、b的值;
(2)若方程f(x)=0有3个不等实根,求c的取值范围.
(1)求a、b的值;
(2)若方程f(x)=0有3个不等实根,求c的取值范围.
分析:(1)根据所给的函数的解析式,对函数求导,使得导函数等于0,得到关于a,b的关系式,解方程组即可,写出函数的解析式.
(2)对函数求导,写出函数的导函数大于0,小于0的x的值,求得f(x)极大值,f(x)极小值,方程f(x)=0有3个不等实根等价于函数y=f(x)的图象与x轴有三个不同的交点,把极值同端点处的值进行比较得到结果.
(2)对函数求导,写出函数的导函数大于0,小于0的x的值,求得f(x)极大值,f(x)极小值,方程f(x)=0有3个不等实根等价于函数y=f(x)的图象与x轴有三个不同的交点,把极值同端点处的值进行比较得到结果.
解答:解:(1)∵f(x)=x3+ax2+bx+c
∴f'(x)=3x2+2ax+b
∵f(x)在x=1,x=3处取得极值
∴f'(1)=3+2a+b=0.f'(3)=27+6a+b=0
∴a=-6,b=9…(6分)
(2)∵f(x)=x3-6x2+9x+c,
∴f'(x)=3x3-12x2+9=3(x-1)(x-3)
∴x∈(-∞,1)时,f'(x)>0,x∈(1,3)时,f'(x)<0,x∈(3,+∞)时,f'(x)>0,
∴f(x)极大值为f(1)=4+c,f(x)极小值为f(3)=c
∴方程f(x)=0有3个不等实根∴函数y=f(x)的图象与x轴有三个不同的交点∴4+c>0>c
∴-4<c<0…(12分)
∴f'(x)=3x2+2ax+b
∵f(x)在x=1,x=3处取得极值
∴f'(1)=3+2a+b=0.f'(3)=27+6a+b=0
∴a=-6,b=9…(6分)
(2)∵f(x)=x3-6x2+9x+c,
∴f'(x)=3x3-12x2+9=3(x-1)(x-3)
∴x∈(-∞,1)时,f'(x)>0,x∈(1,3)时,f'(x)<0,x∈(3,+∞)时,f'(x)>0,
∴f(x)极大值为f(1)=4+c,f(x)极小值为f(3)=c
∴方程f(x)=0有3个不等实根∴函数y=f(x)的图象与x轴有三个不同的交点∴4+c>0>c
∴-4<c<0…(12分)
点评:考查学生利用导数求函数极值的能力,利用导数研究函数单调性的能力,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)的定义域为R,若存在与x无关的正常数M,使|f(x)|≤M|x|对一切实数x恒成立,则称f(x)为有界泛函.有下面四个函数:
①f(x)=1;
②f(x)=x2;
③f(x)=2xsinx;
④![]() .
.
其中属于有界泛函的是( )
|
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
设函数f(![]() )的定义域为R,若存在与
)的定义域为R,若存在与![]() 无关的正常数
无关的正常数![]() ,使
,使![]() 对一切实数
对一切实数![]() 均成立,则称f(
均成立,则称f(![]() )为“有界泛函”,给出以下函数:
)为“有界泛函”,给出以下函数:
|
其中是“有界泛函”的个数为( )
A. 1 B. 2 C .3 D.4
 )的定义域为R,若存在与
)的定义域为R,若存在与 对一切实数
对一切实数 ②f(
②f( ④
④ 其中是“有界泛函”的个数为(
)
其中是“有界泛函”的个数为(
)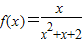 .
.