题目内容
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB= 60°,FC⊥平面ABCD,AE⊥BD,CB=" CD=" CF.
(1)求证:BD⊥平面AED;
(2)求二面角F—BD—C的正切值.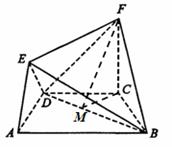
(1)详见解析;(2)2.
解析试题分析:(1)要证明直线和平面垂直,只需证明直线和平面内的两条相交直线垂直.由已知得 ,故只需证明
,故只需证明 ,在
,在 中,由余弦定理得
中,由余弦定理得 的关系,即
的关系,即 的关系确定,在
的关系确定,在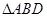 中,结合已知条件
中,结合已知条件 可判定
可判定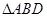 是直角三角形,且
是直角三角形,且 ,从而可证明BD⊥平面AED;(2)求二面角
,从而可证明BD⊥平面AED;(2)求二面角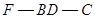 ,可先找后求,过
,可先找后求,过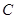 作
作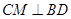 ,由已知FC⊥平面ABCD,得
,由已知FC⊥平面ABCD,得 面
面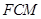 ,故
,故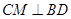 ,
, ,故
,故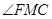 为二面角F—BD—C的平面角,在
为二面角F—BD—C的平面角,在 中计算
中计算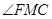 .
.
(1)在等腰梯形ABCD中,AB∥CD,∠DAB= 60°,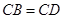 ,由余弦定理可知,
,由余弦定理可知,

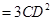 ,即
,即 ,在
,在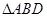 中,
中, ,
,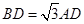 ,则
,则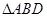 是直角三角形,且
是直角三角形,且 ,又
,又 ,且
,且 ,故BD⊥平面AED.
,故BD⊥平面AED.
(2)过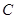 作
作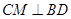 ,交
,交 于点
于点 ,因为FC⊥平面ABCD,
,因为FC⊥平面ABCD, 面
面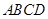 ,所以
,所以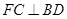 ,所以
,所以 面
面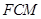 ,因此
,因此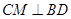 ,
, ,故
,故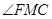 为二面角F—BD—C的平面角.
为二面角F—BD—C的平面角.
在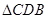 中,
中,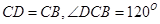 ,可得
,可得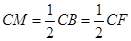
因此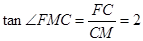 . 即二面角F—BD—C的正切值为2.
. 即二面角F—BD—C的正切值为2.
考点:1、直线和平面垂直的判定;2、二面角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的高为
的高为 ,底面
,底面 是边长为
是边长为 的正方形,顶点
的正方形,顶点 在底面上的射影是正方形
在底面上的射影是正方形 .
. 是棱
是棱 的中点.试求直线
的中点.试求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 .
. 平面
平面 .
.
 ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
, 分别是
分别是 的中点,
的中点, .
. ;
; ;
; 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.
 的侧棱
的侧棱 平面
平面 ,
, 为等边三角形,侧面
为等边三角形,侧面 是正方形,
是正方形, 是
是 的中点,
的中点, 是棱
是棱 上的点.
上的点.
 平面
平面 ;
; 时,求正方形
时,求正方形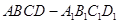 底面
底面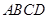 直角梯形,
直角梯形,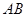 ∥
∥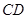 ,
,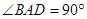 ,
, 是棱
是棱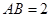 ,
,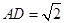 ,
,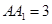 ,
,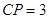 ,
, .
.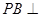 平面
平面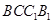 .
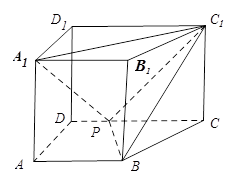
.
 中,
中, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点. 平面
平面 ;
; 平面
平面 ;
; 为正方体
为正方体 的点
的点 的个数,并说明理由.
的个数,并说明理由.
 AB,PH为△PAD边上的高.
AB,PH为△PAD边上的高.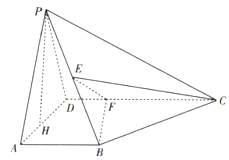
 ,FC=1,求三棱锥E-BCF的体积;
,FC=1,求三棱锥E-BCF的体积; 中,已知
中,已知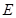 为棱
为棱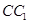 上的动点.
上的动点.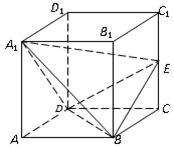
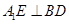 ;
;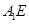 与平面
与平面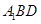 所成角的正弦值.
所成角的正弦值.