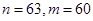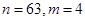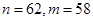题目内容
数列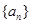 的通项公式
的通项公式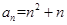 ,则数列
,则数列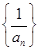 的前10项和为( )
的前10项和为( )
A.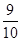 | B.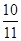 | C.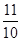 | D.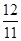 |
B
解析试题分析:因为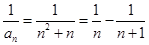 ,所以数列
,所以数列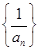 的前
的前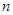 项和
项和 ,所以
,所以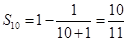 ,选B.
,选B.
考点:数列求和.

练习册系列答案
相关题目
已知函数f(x)=xa的图象过点(4,2),令an=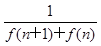 ,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
A.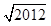 -1 -1 | B. -1 -1 | C.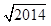 -1 -1 | D.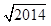 +1 +1 |
已知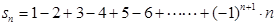 ,则
,则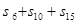 等于( )
等于( )
A.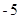 | B.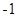 | C. | D. |
已知数列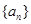 的前n项和
的前n项和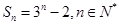 ,则( )
,则( )
A.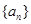 是递增的等比数列 是递增的等比数列 | B.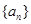 是递增数列,但不是等比数列 是递增数列,但不是等比数列 |
C.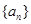 是递减的等比数列 是递减的等比数列 | D.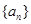 不是等比数列,也不单调 不是等比数列,也不单调 |
已知函数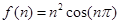 ,且
,且 ,则
,则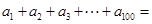 ( )
( )
| A.0 |
| B.100 |
| C.5050 |
| D.10200 |
[2014·宁波质检]化简Sn=n+(n-1)×2+(n-2)×22+…+2×2n-2+2n-1的结果是( )
| A.2n+1-n | B.2n+1-n+2 |
| C.2n-n-2 | D.2n+1-n-2 |
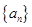 的各项均为正数,且
的各项均为正数,且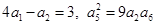 . (1)求数列
. (1)求数列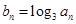 ,求数列
,求数列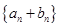 的前
的前 项和
项和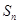 .
.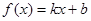 的图像经过点
的图像经过点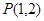 和
和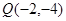 ,令
,令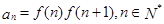 ,记数列
,记数列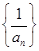 的前项和为
的前项和为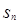 ,当
,当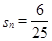 时,
时, 的值等于( )
的值等于( )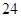
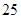
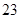
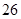
 表示位于从上到下第
表示位于从上到下第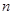 行,从左到右
行,从左到右 列的数 ,比如
列的数 ,比如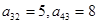 ,若
,若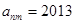 ,则有( )
,则有( )