题目内容
【题目】设函数![]() .
.
(1)当![]() (
(![]() 为自然对数的底数)时,求
为自然对数的底数)时,求![]() 的最小值;
的最小值;
(2)讨论函数![]() 零点的个数.
零点的个数.
【答案】(1)2;(2)见解析
【解析】
(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值即可;
(2)令g(x)=0,得到![]() ;设
;设![]() ,通过讨论m的范围,根据函数的单调性结合函数的草图求出函数的零点个数即可.
,通过讨论m的范围,根据函数的单调性结合函数的草图求出函数的零点个数即可.
解:(1)当m=e时,![]() ,∴
,∴![]()
当x∈(0,e)时,f′(x)<0,f(x)在x∈(0,e)上是减函数;
当x∈(e,+∞)时,f′(x)>0,f(x)在x∈(e,+∞)上是增函;
∴当x=e时,f(x)取最小值![]() .
.
(2)∵函数![]() ,
,
令g(x)=0,得![]() ;
;
设![]() ,则
,则![]() ′(x)=﹣x2+1=﹣(x﹣1)(x+1)
′(x)=﹣x2+1=﹣(x﹣1)(x+1)
当x∈(0,1)时,![]() ′(x)>0,
′(x)>0,![]() (x)在x∈(0,1)上是增函数;
(x)在x∈(0,1)上是增函数;
当x∈(1,+∞)时,![]() ′(x)<0,
′(x)<0,![]() (x)在x∈(1,+∞)上是减函数;
(x)在x∈(1,+∞)上是减函数;
当x=1是![]() (x)的极值点,且是唯一极大值点,∴x=1是
(x)的极值点,且是唯一极大值点,∴x=1是![]() (x)的最大值点;
(x)的最大值点;
∴![]() (x)的最大值为
(x)的最大值为![]() ,又
,又![]() (0)=0结合y=
(0)=0结合y=![]() (x)的图象,
(x)的图象,
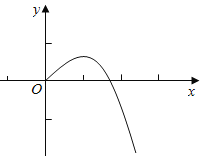
可知:①当![]() 时,函数g(x)无零点;
时,函数g(x)无零点;
②当![]() 时,函数g(x)有且只有一个零点;
时,函数g(x)有且只有一个零点;
③当![]() 时,函数g(x)有两个零点;
时,函数g(x)有两个零点;
④当m≤0时,函数g(x)有且只有一个零点;
综上:当![]() 时,函数g(x)无零点;
时,函数g(x)无零点;
当![]() 或m≤0时,函数g(x)有且只有一个零点;
或m≤0时,函数g(x)有且只有一个零点;
当![]() 时,函数g(x)有且只有两个零点;
时,函数g(x)有且只有两个零点;

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】【安徽省滁州市2018届高三上学期期末考试数学】随着雾霾的日益严重,中国部分省份已经实施了“煤改气”的计划来改善空气质量指数.2017年支撑我国天然气市场消费增长的主要资源是国产常规气和进口天然气,资源每年的增量不足以支撑天然气市场连续![]() 亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在
亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在![]() 亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续
亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数(AQI),数据统计如下:
天监测空气质量指数(AQI),数据统计如下:
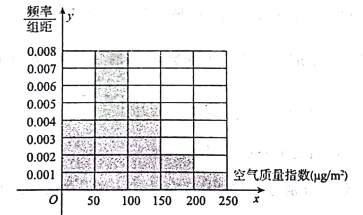
(1)根据上图完成下列表格
空气质量指数( |
|
|
|
|
|
天数 |
(2)若按照分层抽样的方法,从空气质量指数在![]() 以及
以及![]() 的等级中抽取
的等级中抽取![]() 天进行调研,再从这
天进行调研,再从这![]() 天中任取
天中任取![]() 天进行空气颗粒物分析,记这
天进行空气颗粒物分析,记这![]() 天中空气质量指数在
天中空气质量指数在![]() 的天数为
的天数为![]() ,求
,求![]() 的分布列;
的分布列;
(3)以频率估计概率,根据上述情况,若在一年![]() 天中随机抽取
天中随机抽取![]() 天,记空气质量指数在
天,记空气质量指数在![]() 以上(含
以上(含![]() )的天数为
)的天数为![]() ,求
,求![]() 的期望.
的期望.

