题目内容
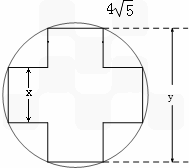
 一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有
一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有 cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
【答案】分析:根据面积求出长,然后表示出外接圆的周长,利用导数研究函数的最小值即可.
解答:解:设外接圆的半径为R cm,则 R=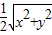 .
.
由2xy-x2=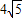 ,得 y=
,得 y=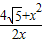 .
.
要使外接圆的周长最小,需要R取最小值,也即R2取最小值.
设 f(x)=R2=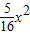 +
+ +
+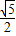 (0<x<2R),则 f'(x)=
(0<x<2R),则 f'(x)= x-
x-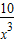 .
.
令f'(x)=0 解得x=2 或x=-2(舍去).
当0<x<2 时f'(x)<0;当x>2 时,f'(x)>0.
因此当x=2时,y=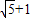 ,R2最小,即R最小,周长最小为π
,R2最小,即R最小,周长最小为π 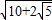 cm.
cm.
点评:本题通过设间接变量,由题意得到一个函数,再确定它的最小值.间接处理所研究的目标,并用导数研究目标函数的最小值,是解本题的关键所在.
解答:解:设外接圆的半径为R cm,则 R=
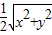 .
.由2xy-x2=
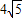 ,得 y=
,得 y=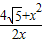 .
.要使外接圆的周长最小,需要R取最小值,也即R2取最小值.
设 f(x)=R2=
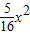 +
+ +
+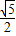 (0<x<2R),则 f'(x)=
(0<x<2R),则 f'(x)= x-
x-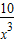 .
.令f'(x)=0 解得x=2 或x=-2(舍去).
当0<x<2 时f'(x)<0;当x>2 时,f'(x)>0.
因此当x=2时,y=
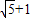 ,R2最小,即R最小,周长最小为π
,R2最小,即R最小,周长最小为π 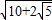 cm.
cm.点评:本题通过设间接变量,由题意得到一个函数,再确定它的最小值.间接处理所研究的目标,并用导数研究目标函数的最小值,是解本题的关键所在.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
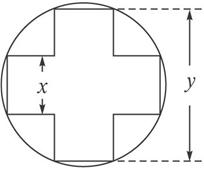
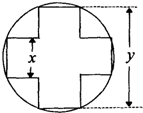 (2012•河北模拟)一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有
(2012•河北模拟)一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽 及长
及长 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
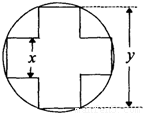
 cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.