题目内容
设数列
的各项均为正数，若对任意的正整数
，都有
成等差数列，且
成等比数列．
（Ⅰ）求证数列
是等差数列；
（Ⅱ）如果
，求数列
的前项和。
（Ⅰ）见解析 （Ⅱ） 
解析:
（Ⅰ）由题意，得
， ①
， ② …………2分
因为
，所以由式②得
， 从而当
时，
，
代入式①得
， ……4分
故当
时，
，
数列
是等差数列． ………………6分
（II）由
及式①、②易得
因此的公差
，从而
，………8分
得
， 所以当时，
， ③
又
也适合式③， 
.
………10分
设数列
的前
项和为 
.
=
=
…………12分
练习册系列答案
相关题目
的各项均为正数，前
项和为
，对于任意的
，
成等差数列，设数列
的前
，且
，则对任意的实数
（
是自然对数的底）和任意正整数
B．
C．
D．
的各项均为正数.若对任意的
，存在
，使得
成立，则称数列
，
，求
；
，
，
，
，…成等比数列，且公比
，
}是“j4型”数列，得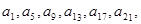
，…成等比数列，设公比为t. 由{
，…成等比数列，设公比为
；
，…成等比数列，设公比为
；
…成等比数列，设公比为
；
的各项均为正数，若对任意的正整数
，都有
成等差数列，且
成等比数列．
是等差数列；
，求数列错误！不能通过编辑域代码创建对象。的前错误！不能通过编辑域代码创建对象。项和。