题目内容
10.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,b∈Z)的右焦点为F($\sqrt{5}$,0),短轴长与椭圆上顶点到右准线的距离之比为$\frac{4\sqrt{5}}{9}$.(1)求椭圆的方程;
(2)过点P(0,3)引直线l顺次交椭圆于M、N两点,求|MN|取值范围.
分析 (1)由椭圆的右焦点为F($\sqrt{5}$,0),可得c=$\sqrt{5}$.短轴长与椭圆上顶点到右准线的距离之比为$\frac{4\sqrt{5}}{9}$.可得$\frac{2b}{\frac{{a}^{2}}{c}}=\frac{4\sqrt{5}}{9}$.又b∈Z,b2=a2-c2,解出即可.
(2)当直线l的斜率不存在时,|MN|=2b=4.当直线l的斜率存在时,设直线l的方程为:y=kx+3,(不妨取k>0),代入椭圆方程可得:(4+9k2)x2+54kx+45=0.△>0,利用根与系数的关系可得|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$,通过换元利用函数的单调性即可得出.
解答 解:(1)由椭圆的右焦点为F($\sqrt{5}$,0),∴c=$\sqrt{5}$.
短轴长与椭圆上顶点到右准线的距离之比为$\frac{4\sqrt{5}}{9}$.
∴$\frac{2b}{\frac{{a}^{2}}{c}}=\frac{4\sqrt{5}}{9}$.又b∈Z,b2=a2-c2,
解得:b=2,a=3.
∴椭圆的方程为:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$.
(2)当直线l的斜率不存在时,|MN|=2b=4.
当直线l的斜率存在时,设直线l的方程为:y=kx+3,(不妨取k>0)
代入椭圆方程可得:(4+9k2)x2+54kx+45=0.
△>0,解得k2$>\frac{5}{9}$.
∴x1+x2=$\frac{-54k}{4+9{k}^{2}}$,x1x2=$\frac{45}{4+9{k}^{2}}$.
∴|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\frac{12\sqrt{(1+{k}^{2})(9{k}^{2}-5)}}{4+9{k}^{2}}$,
∵k2$>\frac{5}{9}$,∴|MN|>0.
令${k}^{2}+1=t>\frac{14}{9}$,
则|MN|=$12\sqrt{\frac{1}{9+\frac{36t+25}{9{t}^{2}-14t}}}$<$12\sqrt{\frac{1}{9}}$=4,
综上可得:0<|MN|≤4.
∴|MN|取值范围是(0,4].
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立化为一元二次方程的根与系数的关系、弦长公式,考查了分类讨论思想方法、推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{5}$ | B. | $\frac{6}{5}$ | C. | 2 | D. | 6$\sqrt{2}$-1 |
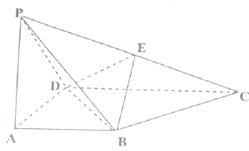 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA=AD=AB=1,CD=2,E为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA=AD=AB=1,CD=2,E为PC的中点.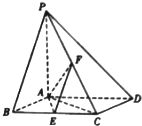 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.