[题目]如图.直角坐标系x′Oy所在的平面为β.直角坐标系xOy所在的平面为α.且二面角α﹣y轴﹣β的大小等于30°．已知β内的曲线C′的方程是3(x﹣2 )2+4y2﹣36=0.则曲线C′在α内的射影在坐标系xOy下的曲线方程是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，直角坐标系x′Oy所在的平面为β，直角坐标系xOy所在的平面为α，且二面角α﹣y轴﹣β的大小等于30°．已知β内的曲线C′的方程是3（x﹣2 ）2+4y2﹣36=0，则曲线C′在α内的射影在坐标系xOy下的曲线方程是．

【答案】（x﹣3）2+y2=9
【解析】解：设3（x﹣2 ）2+4y2﹣36=0上的任意点为A（x，y），
A在平面α上的射影是（x，y）
∵直角坐标系x′Oy所在的平面为β，
直角坐标系xOy所在的平面为α，且二面角α﹣y轴﹣β的大小等于30°．
∴根据题意，得到x= x，y=y，
∵3（x﹣2 ）2+4y2﹣36=0，
∴3（ x﹣2 ）2+4y2﹣36=0
∴（x﹣3）2+y2=9
所以答案是：（x﹣3）2+y2=9．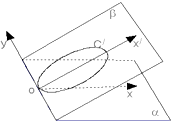

练习册系列答案

相关题目

【题目】已知函数f（x）=log2x，g（x）=x2+2x，数列{an}的前n项和记为Sn ， bn为数列{bn}的通项，n∈N* ．点（bn ， n）和（n，Sn）分别在函数f（x）和g（x）的图象上．
（1）求数列{an}和{bn}的通项公式；
（2）令Cn= ，求数列{Cn}的前n项和Tn ．

【题目】阅读下面材料，尝试类比探究函数y=x2﹣ 的图象，写出图象特征，并根据你得到的结论，尝试猜测作出函数对应的图象．阅读材料：
我国著名数学家华罗庚先生曾说：数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事休．
在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来琢磨函数的图象的特征．我们来看一个应用函数的特征研究对应图象形状的例子．
对于函数y= ，我们可以通过表达式来研究它的图象和性质，如：

（1）在函数y= 中，由x≠0，可以推测出，对应的图象不经过y轴，即图象与y轴不相交；由y≠0，可以推测出，对应的图象不经过x轴，即图象与x轴不相交．
（2）在函数y= 中，当x＞0时y＞0；当x＜0时y＜0，可以推测出，对应的图象只能在第一、三象限；
（3）在函数y= 中，若x∈（0，+∞）则y＞0，且当x逐渐增大时y逐渐减小，可以推测出，对应的图象越向右越靠近x轴；若x∈（﹣∞，0），则y＜0，且当x逐渐减小时y逐渐增大，可以推测出，对应的图象越向左越靠近x轴；
（4）由函数y= 可知f（﹣x）=﹣f（x），即y= 是奇函数，可以推测出，对应的图象关于原点对称．结合以上性质，逐步才想出函数y= 对应的图象，如图所示，在这样的研究中，我们既用到了从特殊到一般的思想，由用到了分类讨论的思想，既进行了静态（特殊点）的研究，又进行了动态（趋势性）的思考．让我们享受数学研究的过程，传播研究数学的成果．