题目内容
动圆C的方程为x2+y2+2ax-4ay+5=0.(1)若a=2,且直线y=3x与圆C交于A,B两点,求弦长|AB|;
(2)求动圆圆心C的轨迹方程;
(3)若直线y=kx-2k与动圆圆心C的轨迹有公共点,求k的取值范围.
【答案】分析:化x2+y2+2ax-4ay+5=0为标准方程,
(1)a=2时,与y=3x联立,求出A,B的坐标,由两点间距离公式,可得结论;
(2)动圆圆心为(-a,2a),可求动圆圆心C的轨迹方程;
(3)直线y=kx-2k=k(x-2)过定点(2,0),可得结论.
解答:解:化x2+y2+2ax-4ay+5=0为标准方程得:(x+a)2+(y-2a)2=5a2-5
(1)a=2时,圆方程为:(x+2)2+(y-4)2=15与y=3x联立解得x1=1+ ,y1=3+
,y1=3+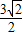 ;x2=1-
;x2=1-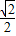 ,y2=3-
,y2=3- ,即A(1+
,即A(1+ ,3+
,3+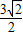 )、B(1-
)、B(1-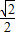 ,3-
,3- ),
),
由两点间距离公式,得|AB|=2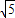 ;
;
(2)动圆圆心为(-a,2a),所以x=-a,y=2a,即y=-2x;
(3)因直线y=kx-2k=k(x-2)过定点(2,0),又与y=-2x有公共点,所以k≠-2(因为k=-2时两条直线平行).
点评:本题考查圆的方程,考查轨迹方程,考查学生分析解决问题的能力,属于中档题.
(1)a=2时,与y=3x联立,求出A,B的坐标,由两点间距离公式,可得结论;
(2)动圆圆心为(-a,2a),可求动圆圆心C的轨迹方程;
(3)直线y=kx-2k=k(x-2)过定点(2,0),可得结论.
解答:解:化x2+y2+2ax-4ay+5=0为标准方程得:(x+a)2+(y-2a)2=5a2-5
(1)a=2时,圆方程为:(x+2)2+(y-4)2=15与y=3x联立解得x1=1+
 ,y1=3+
,y1=3+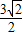 ;x2=1-
;x2=1-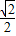 ,y2=3-
,y2=3- ,即A(1+
,即A(1+ ,3+
,3+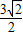 )、B(1-
)、B(1-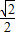 ,3-
,3- ),
),由两点间距离公式,得|AB|=2
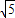 ;
;(2)动圆圆心为(-a,2a),所以x=-a,y=2a,即y=-2x;
(3)因直线y=kx-2k=k(x-2)过定点(2,0),又与y=-2x有公共点,所以k≠-2(因为k=-2时两条直线平行).
点评:本题考查圆的方程,考查轨迹方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目