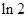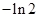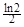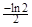题目内容
若函数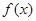 为定义在R上的奇函数,且在(0,+
为定义在R上的奇函数,且在(0,+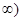 为增函数,又
为增函数,又
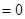 ,则不等式
,则不等式 的解集为
的解集为
A.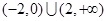 | B.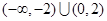 |
C.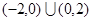 | D.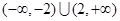 |
D
解析试题分析:因为函数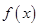 在
在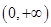 为增函数,且
为增函数,且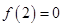 ,所以当
,所以当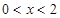 时
时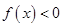 ,当
,当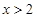 时
时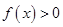 ,又函数
,又函数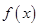 为
为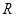 上的奇函数,所以函数
上的奇函数,所以函数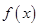 在
在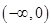 上亦为增函数,且当
上亦为增函数,且当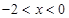 时
时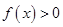 ,当
,当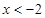 时
时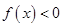 ,又由
,又由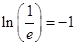 ,所以不等式
,所以不等式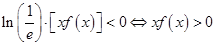 ,故所求不等式的解集为
,故所求不等式的解集为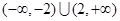 .所以正确答案为D.
.所以正确答案为D.
考点:1.函数奇偶性;2.函数单调性;3.不等式的解.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
设函数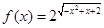 ,对于给定的正数
,对于给定的正数 ,定义函数
,定义函数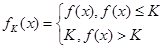 若对于函数
若对于函数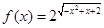 定义域内的任意
定义域内的任意 ,恒有
,恒有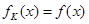 ,则( )
,则( )
A. 的最大值为 的最大值为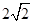 | B. 的最小值为 的最小值为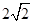 |
C. 的最大值为1 的最大值为1 | D. 的最小值为1 的最小值为1 |
设方程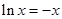 与方程
与方程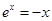 (其中e是自然对数的底数)的所有根之和为
(其中e是自然对数的底数)的所有根之和为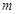 ,则( )
,则( )
A.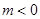 | B.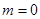 | C.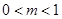 | D.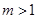 |
记实数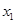 ,
,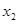 ,…,
,…,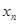 中的最大数为
中的最大数为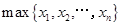 ,最小数为
,最小数为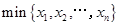 ,则
,则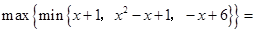 ( )
( )
A. | B.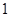 | C.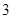 | D.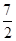 |
函数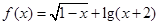 的定义域为
的定义域为
A.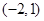 | B.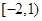 | C.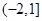 | D.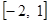 |
已知 是定义在
是定义在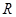 上的奇函数,当
上的奇函数,当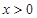 时,
时,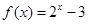 ,那么
,那么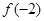 的值是( )
的值是( )
A.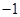 | B.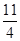 | C.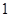 | D.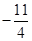 |
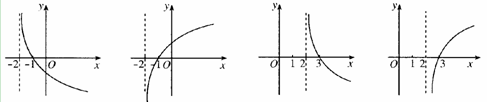
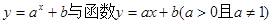 的图像有可能是( )
的图像有可能是( )
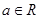 ,函数
,函数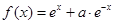 的导函数是
的导函数是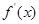 ,且
,且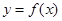 的一条切线的斜率是
的一条切线的斜率是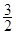 ,则切点的横坐标为( )
,则切点的横坐标为( )