题目内容
已知函数y=a1-x(a>0,a≠1)的图象恒过定点A,若点A在直线 (m>0,n>0)上,则m+n的最小值为 .
(m>0,n>0)上,则m+n的最小值为 .
【答案】分析:求出定点A(1,1),由点A在直线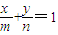 (m>0,n>0)上,可得
(m>0,n>0)上,可得  ,再由 m+n=( m+n)(
,再由 m+n=( m+n)( )=2+
)=2+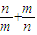 ,利用基本不等式求出m+n的最小值.
,利用基本不等式求出m+n的最小值.
解答:解:∵函数y=a1-x(a>0,a≠1)的图象恒过定点A(1,1),点A在直线 (m>0,n>0)上,
(m>0,n>0)上,
∴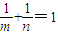 ,∴m+n=( m+n)(
,∴m+n=( m+n)( )=2+
)=2+ .
.
∵m>0,n>0,由基本不等式可得 ≥2,当且仅当
≥2,当且仅当 时,等号成立.
时,等号成立.
再由 可得,当且仅当 m=n=2时,等号成立.
可得,当且仅当 m=n=2时,等号成立.
故 m+n=2+ ≥4,当且仅当 m=n=2时,等号成立.
≥4,当且仅当 m=n=2时,等号成立.
故m+n的最小值为4,
故答案为 4.
点评:本题主要考查指数函数的单调性和特殊点,基本不等式的应用,得到 m+n=( m+n)( ),是解题的关键,属于基础题.
),是解题的关键,属于基础题.
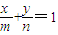 (m>0,n>0)上,可得
(m>0,n>0)上,可得  ,再由 m+n=( m+n)(
,再由 m+n=( m+n)( )=2+
)=2+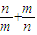 ,利用基本不等式求出m+n的最小值.
,利用基本不等式求出m+n的最小值.解答:解:∵函数y=a1-x(a>0,a≠1)的图象恒过定点A(1,1),点A在直线
 (m>0,n>0)上,
(m>0,n>0)上,∴
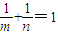 ,∴m+n=( m+n)(
,∴m+n=( m+n)( )=2+
)=2+ .
.∵m>0,n>0,由基本不等式可得
 ≥2,当且仅当
≥2,当且仅当 时,等号成立.
时,等号成立.再由
 可得,当且仅当 m=n=2时,等号成立.
可得,当且仅当 m=n=2时,等号成立.故 m+n=2+
 ≥4,当且仅当 m=n=2时,等号成立.
≥4,当且仅当 m=n=2时,等号成立.故m+n的最小值为4,
故答案为 4.
点评:本题主要考查指数函数的单调性和特殊点,基本不等式的应用,得到 m+n=( m+n)(
 ),是解题的关键,属于基础题.
),是解题的关键,属于基础题. 
练习册系列答案
相关题目