Question

【题目】已知函数f(x)=x2﹣alnx，a>0.

（1）若f(x)在x=1处取得极值，求实数a的值；

（2）求f(x)在区间[2，+∞)上的最小值；

（3）在（1）的条件下，若g(x)=x2﹣f(x)，求证:当1<x<e2，恒有x.

Answer 1

【答案】（1）2（2）当0<a≤8时，最小值为4﹣2ln2；当a>8时，最小值为（3）证明见解析

【解析】

（1）利用列方程，由此求得的可能取值，验证后求得的值.

（2）求得的定义域和导函数，根据两种情况进行分类讨论，结合函数的单调区间，求得在区间上的最小值.

（3）求得，判断出，将要证明的不等式转化为，构造函数，利用导数证得，由此证得不等式成立.

（1）由f(x)=x2﹣alnx知，函数的定义域为(0，+∞)，，∵函数f(x)在x=1处取得极值，∴f′(1)=0，即2﹣a=0，解得a=2，经检验，满足题意，故a=2；

（2）由（1）得，定义域为(0，+∞)，当0<a≤8时，由f′(x)=0得，且，当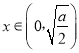时，f′(x)<0，f(x)单调递减，当时，f′(x)>0，f(x)单调递增，∴f(x)在区间[2，+∞)上单调递增，最小值为f(2)=4﹣2ln2，当a>8时，，当时，f′(x)<0，f(x)单调递减，当时，f′(x)>0，f(x)单调递增，∴函数f(x)在处取得最小值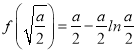，综上，当0<a≤8时，f(x)在区间[2，+∞)上的最小值为4﹣2ln2；当a>8时，f(x)在区间[2，+∞)上的最小值为；

（3）由g(x)=x2﹣f(x)得g(x)=2lnx，当1<x<e2时，0<lnx<2，0<g(x)<4，欲证，只需证x[4﹣g(x)]<4+g(x)，即证，即，设，则，当1<x<e2时，φ′(x)>0，所以φ(x)在区间(1，e2)上单调递增，∴φ(x)>φ(1)=0，即，∴，由此得证.