题目内容
对于半径为r的圆,由(πr2)'=2πr可以得到结论:圆的面积关于半径的函数的导数等于圆的周长关于半径的函数,通过类比可以得到:对于半径为r 的球,由
πr2)
类比推理
类比推理
,可以得到结论球的体积函数的导数等于球的表面积函数
球的体积函数的导数等于球的表面积函数
(参考公式:球的体积公式V=| 4 | 3 |
分析:圆的面积函数的导数等于圆的周长函数,类比得到球的体积函数的导数等于球的表面积函数,有二维空间推广到三维空间.
解答:解:V球=
πR3,又 (
πR3)′=4πR2
用语言叙述为“球的体积函数的导数等于球的表面积函数.”
即,可由类比推理可得“球的体积函数的导数等于球的表面积函数.”
故答案为:类比推理,球的体积函数的导数等于球的表面积函数.
| 4 |
| 3 |
| 4 |
| 3 |
用语言叙述为“球的体积函数的导数等于球的表面积函数.”
即,可由类比推理可得“球的体积函数的导数等于球的表面积函数.”
故答案为:类比推理,球的体积函数的导数等于球的表面积函数.
点评:本题考查类比推理,解答本题的关键是:(1)找出两类事物:圆与球之间的相似性或一致性;(2)用圆的性质去推测球的性质,得出一个明确的命题(猜想).

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目

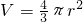 )
)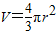 )
)