题目内容
若平面上三点A、B、C满足|| AB |
| BC |
| CA |
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
分析:根据
+
+
=0可得,(
+
+
)2=0,展开可得|
|2+|
|2+|
|2+2(
•
+
•
+
•
)=0,代入即可得到答案.
| AB |
| BC |
| CA |
| AB |
| BC |
| CA |
| AB |
| BC |
| CA |
| AB |
| BC |
| AB |
| AC |
| BC |
| AC |
解答:解:由
+
+
=0可得(
+
+
)2=0,
∵|
|=3,|
|=4,|
|=5
|
|2+|
|2+|
|2+2(
•
+
•
+
•
)=0,
9+16+25+2(
•
+
•
+
•
)=0
∴
•
+
•
•
=-25.
故答案为:-25
| AB |
| BC |
| CA |
| AB |
| BC |
| CA |
∵|
| AB |
| BC |
| CA |
|
| AB |
| BC |
| CA |
| AB |
| BC |
| AB |
| AC |
| BC |
| AC |
9+16+25+2(
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
∴
| AB |
| BC |
| BC |
| CA |
| AB |
故答案为:-25
点评:本题主要考查向量的数量积运算.多注意一些巧妙的转化.

练习册系列答案
相关题目
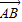 |=3,|
|=3,|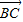 |=4,|
|=4,|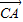 |=5,则
|=5,则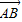 •
• +
+ •
•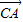 +
+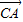 •
•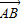 的值等于 .
的值等于 .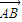 |=3,|
|=3,|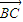 |=4,|
|=4,|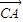 |=5,则
|=5,则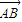 •
• +
+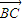 •
•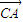 +
+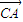 •
•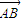 的值等于 .
的值等于 .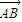 |=3,|
|=3,|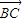 |=4,|
|=4,|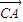 |=5,则
|=5,则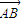 •
•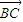 +
+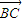 •
•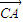 +
+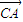 •
•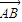 的值等于 .
的值等于 .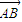 |=3,|
|=3,|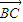 |=4,|
|=4,|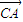 |=5,则
|=5,则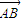 •
•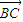 +
+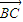 •
•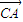 +
+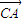 •
• 的值等于 .
的值等于 .