题目内容
某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试(满分150分),若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)若通过学校选拔测试的学生将代表学校参加市知识竞赛,知识竞赛分为初赛和复赛,初赛中每人最多有5次答题机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.假设参赛者甲答对每一个题的概率都是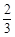 ,求甲在初赛中答题个数的分布列和数学期望.
,求甲在初赛中答题个数的分布列和数学期望.
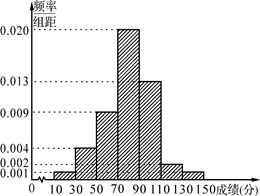
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)若通过学校选拔测试的学生将代表学校参加市知识竞赛,知识竞赛分为初赛和复赛,初赛中每人最多有5次答题机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.假设参赛者甲答对每一个题的概率都是
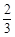 ,求甲在初赛中答题个数的分布列和数学期望.
,求甲在初赛中答题个数的分布列和数学期望.
(1) ;(2)
;(2) 的分布列为
的分布列为
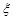 数学期望
数学期望 .
.
 ;(2)
;(2)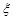 的分布列为
的分布列为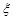 | 3 | 4 | 5 |
| p |  |  |  |
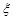 数学期望
数学期望 .
.试题分析:(1)利用频率分布直方图求平均值,取各组的中间值,乘以各组的频率再相加即得,即
 ,其中
,其中 为第
为第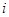 组数据的频率,
组数据的频率,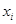 是第
是第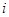 组数据的中间值.(2)首先确定随机变量的所有可能值.记甲在初赛中的答题个数为随机变量
组数据的中间值.(2)首先确定随机变量的所有可能值.记甲在初赛中的答题个数为随机变量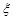 ,显然他至少都要答3个题,最多答5个题.所以
,显然他至少都要答3个题,最多答5个题.所以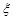 的可能值为3,4,5,
的可能值为3,4,5, 表示前3个题都答对或都答错;
表示前3个题都答对或都答错;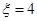 表示前3个题中恰好答对2个且第4个答对或前3个题中恰好答错2个且第4个答错;
表示前3个题中恰好答对2个且第4个答对或前3个题中恰好答错2个且第4个答错;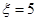 表示前4个题中恰好答对2个.据此即可求出
表示前4个题中恰好答对2个.据此即可求出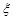 的分布列及期望.
的分布列及期望. (1)设平均成绩的估计值为
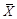 ,则:
,则:
 . 4分
. 4分(2)记甲在初赛中的答题个数为随机变量
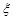 ,这
,这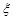 的可能值为3,4,5,
的可能值为3,4,5, ,
,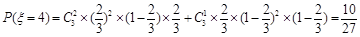 ,
, (或
(或 ).
).10分
则
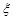 的分布列为
的分布列为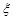 | 3 | 4 | 5 |
| p |  |  |  |
所以
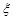 数学期望
数学期望 . 12分
. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 天)的空气质量指数
天)的空气质量指数 监测数据,统计结果如下:
监测数据,统计结果如下:









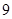

 (单位:元)与空气质量指数
(单位:元)与空气质量指数 )的
)的
 元且不超过
元且不超过 元的概率.
元的概率.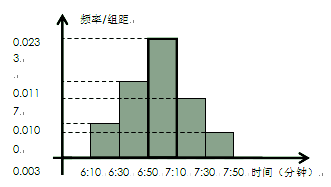
 ;
;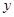 在上午
在上午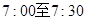 之间,而送报人每天在
之间,而送报人每天在 )的概率;
)的概率;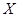 的数学期望.
的数学期望. 次预赛成绩记录如下:
次预赛成绩记录如下: 

 乙
乙 


 名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示: ,由此请估计出山高为72(km)处气温的度数为( )
,由此请估计出山高为72(km)处气温的度数为( )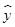 =0.50x-0.81,则x=25时,
=0.50x-0.81,则x=25时, 在
在 时的值时,
时的值时, 的值为
的值为