题目内容
16、“三角形的三条中线交于一点，且这一点到顶点的距离等于它到对边中点距离的2倍”试类比：四面体的四条中线（顶点到对面三角形重心的连线段）交于一点，且这一点到顶点的距离等于它到对面重心距离的
3
倍．分析：本题考察的知识点是类比推理，由平面图形的性质类比猜想空间几何体的性质，一般的思路是：点到线，线到面，或是二维变三维；由题目中三角形的三条中线交于一点，且这一点到顶点的距离等于它到对边中点距离的2倍的结论是二维线段长与线段长的关系，类比后的结论应该为三维的边与边的比例关系．
解答：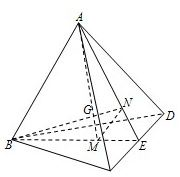
解：由平面图形的性质类比猜想空间几何体的性质，
一般的思路是：点到线，线到面，或是二维变三维；
由题目中“三角形的三条中线交于一点，且这一点到顶点的距离等于它到对边中点距离的2倍”，
我们可以推断：“四面体的四条中线（顶点到对面三角形重心的连线段）交于一点，且这一点到顶点的距离等于它到对面重心距离的3倍．”
如图，△ABE中，M、N为AE、BE的三等分点，
∴MN∥AB，AB=3MN，∴AG=3GM．（用正四面体验证也可）
故答案为：3．
解：由平面图形的性质类比猜想空间几何体的性质，一般的思路是：点到线，线到面，或是二维变三维；
由题目中“三角形的三条中线交于一点，且这一点到顶点的距离等于它到对边中点距离的2倍”，
我们可以推断：“四面体的四条中线（顶点到对面三角形重心的连线段）交于一点，且这一点到顶点的距离等于它到对面重心距离的3倍．”
如图，△ABE中，M、N为AE、BE的三等分点，
∴MN∥AB，AB=3MN，∴AG=3GM．（用正四面体验证也可）
故答案为：3．
点评：本题主要考查类比推理的知识点，解答本题的关键是由平面图形的性质类比猜想空间几何体的性质．类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．
练习册系列答案
相关题目
下列语句中，不能成为命题的是（ ）
| A、5＞12 | ||||||||
| B、x＞0 | ||||||||
C、若
| ||||||||
| D、三角形的三条中线交于一点 |