Question

在极坐标系中，已知圆C的圆心C(3,)，半径为1.Q点在圆周上运动，O为极点.

(1)求圆C的极坐标方程；

(2)若P在直线OQ上运动，且满足，求动点P的轨迹方程.

Answer 1

解析:在△OCQ中,根据余弦定理,可找到圆C上的任意一点Q的ρ、θ之间的关系；通过比例,可找到Q点与P点极坐标之间的关系,从而求出点P的轨迹方程.?

解:(1)设Q(ρ,θ)为圆C上任意一点,如图,在△OCQ中,|OC|=3,|OQ|=ρ,|CQ|=1,∠COQ=|θ-|,根据余弦定理,得1=ρ²+9-2·ρ·3·cos|θ-|,化简整理,得ρ²-6·ρcos(θ-)+8=0为圆C的轨迹方程.?

(2)设Q(ρ₁,θ₁),则有ρ₁²-6·ρ₁cos(θ₁-)+8=0.           ①?

设P(ρ,θ),则OQ∶QP=ρ₁∶(ρ-ρ₁)=2∶3ρ₁=ρ.又θ₁=θ,即?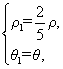

代入①得ρ²-6·ρcos(θ-)+8=0,?

整理得ρ²-15ρcos(θ-)+50=0为P点的轨迹方程.