题目内容
求经过直线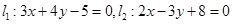 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程:
(1)与直线2x+3y+5=0平行;
(2)与直线2x+3y+5=0垂直.
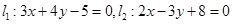 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程:(1)与直线2x+3y+5=0平行;
(2)与直线2x+3y+5=0垂直.
(1)2x+3y-4=0;(2)3x-2y+7=0.
试题分析:(1)与直线2x+3y+5=0平行的直线假设为2x+3y+c=0平行,代入交点坐标即可求出c的值.(2)与直线2x+3y+5=0垂直的直线假设为3x-2y+b=0,代入交点解出b的值即可.
试题解析:由题意知:两条直线的交点为(-1,2),
(1)因为过(-1,2),所以与2x+3y+5=0平行的直线为2x+3y-4=0.
(2)设与2x+3y+5=0垂直的直线方程为3x-2y+b=0,又过点(-1,2),代入得b=7,故,直线方程为3x-2y+7=0.本题考查与已知直线平行的直线的假设技巧,与已知直线垂直的直线的假设技巧.这种方法要熟练.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
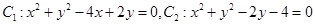 交于
交于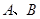 两点.
两点.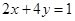 上的圆的方程.
上的圆的方程.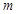 取何实数,直线
取何实数,直线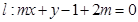 恒过一定点,则该定点的坐标为( )
恒过一定点,则该定点的坐标为( )



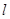 过点(-1,2)且在两坐标上的截距相等,则
过点(-1,2)且在两坐标上的截距相等,则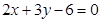 关于直线
关于直线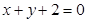 对称的直线方程为______ __.
对称的直线方程为______ __.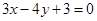 与
与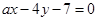 的距离为 .
的距离为 .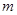 被两条平行直线
被两条平行直线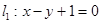 与
与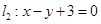 所截得的线段长为
所截得的线段长为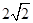 ,则直线
,则直线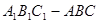 中,
中,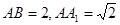 ,则
,则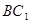 与面
与面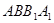 所成的角大小是( )
所成的角大小是( )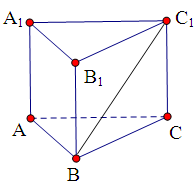
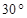


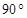
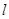 被两平行直线
被两平行直线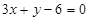
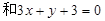 所截得的线段长为3,且直线过点(1,0),求直线
所截得的线段长为3,且直线过点(1,0),求直线