题目内容
已知不等式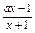 >0 (a∈R).
>0 (a∈R).
(1)解这个关于x的不等式;
(2)若x=-a时不等式成立,求a的取值范围.
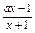 >0 (a∈R).
>0 (a∈R).(1)解这个关于x的不等式;
(2)若x=-a时不等式成立,求a的取值范围.
(1)a<-1时,解集为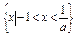 ;a=-1时,原不等式无解;-1<a<0时,解集为
;a=-1时,原不等式无解;-1<a<0时,解集为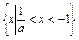 ;a=0时,解集为{x|x<-1};a>0时,解集为
;a=0时,解集为{x|x<-1};a>0时,解集为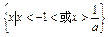 .
.
(2)a的取值范围为a>1
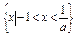 ;a=-1时,原不等式无解;-1<a<0时,解集为
;a=-1时,原不等式无解;-1<a<0时,解集为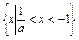 ;a=0时,解集为{x|x<-1};a>0时,解集为
;a=0时,解集为{x|x<-1};a>0时,解集为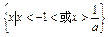 .
.(2)a的取值范围为a>1
(1)原不等式等价于(ax-1)(x+1)>0.
①当a=0时,由-(x+1)>0,得x<-1;
②当a>0时,不等式化为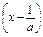 (x+1)>0,
(x+1)>0,
解得x<-1或x>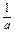 ;
;
③当a<0时,不等式化为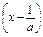 (x+1)<0;
(x+1)<0;
若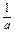 <-1,即-1<a<0,则
<-1,即-1<a<0,则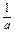 <x<-1;
<x<-1;
若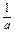 =-1,即a=-1,则不等式解集为空集;
=-1,即a=-1,则不等式解集为空集;
若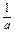 >-1,即a<-1,则-1<x<
>-1,即a<-1,则-1<x<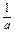 .
.
综上所述,a<-1时,解集为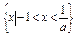 ;a=-1时,原不等式无解;-1<a<0时,解集为
;a=-1时,原不等式无解;-1<a<0时,解集为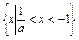 ;a=0时,解集为{x|x<-1};a>0时,解集为
;a=0时,解集为{x|x<-1};a>0时,解集为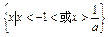 .
.
(2)∵x=-a时不等式成立,
∴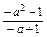 >0,即-a+1<0,
>0,即-a+1<0,
∴a>1,即a的取值范围为a>1.
①当a=0时,由-(x+1)>0,得x<-1;
②当a>0时,不等式化为
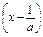 (x+1)>0,
(x+1)>0,解得x<-1或x>
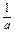 ;
;③当a<0时,不等式化为
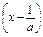 (x+1)<0;
(x+1)<0;若
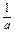 <-1,即-1<a<0,则
<-1,即-1<a<0,则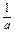 <x<-1;
<x<-1;若
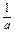 =-1,即a=-1,则不等式解集为空集;
=-1,即a=-1,则不等式解集为空集;若
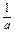 >-1,即a<-1,则-1<x<
>-1,即a<-1,则-1<x<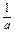 .
.综上所述,a<-1时,解集为
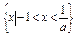 ;a=-1时,原不等式无解;-1<a<0时,解集为
;a=-1时,原不等式无解;-1<a<0时,解集为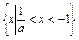 ;a=0时,解集为{x|x<-1};a>0时,解集为
;a=0时,解集为{x|x<-1};a>0时,解集为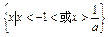 .
.(2)∵x=-a时不等式成立,
∴
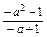 >0,即-a+1<0,
>0,即-a+1<0,∴a>1,即a的取值范围为a>1.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
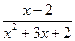 的解集是 .
的解集是 .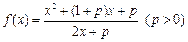
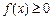 ;
;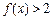 对
对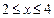 时恒成立,求p的范围.
时恒成立,求p的范围.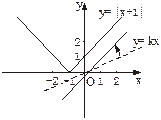
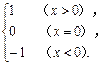 当x∈R时,解不等式(x+2)>(2x-1)sgnx.
当x∈R时,解不等式(x+2)>(2x-1)sgnx.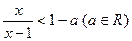
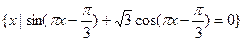 ,若
,若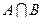 恰有3个元素,求a的取值范围。
恰有3个元素,求a的取值范围。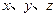 均为正实数,则
均为正实数,则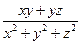 的最大值为 ( )
的最大值为 ( )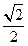
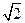
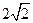
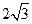
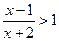 的解集是 。
的解集是 。