题目内容
18.已知数列{an}的通项公式为an=$\frac{1}{n^2+3n}$,求数列{an}前n项和Sn.分析 由an=$\frac{1}{n^2+3n}$=$\frac{1}{3}(\frac{1}{n}-\frac{1}{n+3})$,利用“裂项求和”即可得出.
解答 解:∵an=$\frac{1}{n^2+3n}$=$\frac{1}{3}(\frac{1}{n}-\frac{1}{n+3})$,
∴数列{an}前n项和Sn=$\frac{1}{3}[(1-\frac{1}{4})+(\frac{1}{2}-\frac{1}{5})+(\frac{1}{3}-\frac{1}{6})+(\frac{1}{4}-\frac{1}{7})$+…+$(\frac{1}{n-3}-\frac{1}{n})$+$(\frac{1}{n-2}-\frac{1}{n+1})$+$(\frac{1}{n-1}-\frac{1}{n+2})$+$(\frac{1}{n}-\frac{1}{n+3})]$
=$\frac{1}{3}(1+\frac{1}{2}+\frac{1}{3}$-$\frac{1}{n+1}-\frac{1}{n+2}-\frac{1}{n+3})$
=$\frac{1}{3}(\frac{11}{6}$-$\frac{1}{n+1}-\frac{1}{n+2}-\frac{1}{n+3})$
点评 本题考查了数列的“裂项求和”方法、变形能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若函数f(x)=alnx(a>0)的图象在x=1处的切线与圆x2+y2=b2(b>0)相切,则$\frac{1}{{b}^{2}}$-$\frac{1}{{a}^{2}}$等于( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
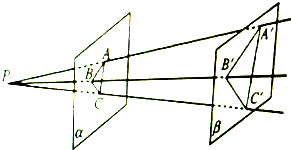 如图,从平面ABC外一点P,引射线PA、PB、PC,在它们上面分别取点A′、B′、C′,使$\frac{PA}{PA′}$=$\frac{PB}{PB′}$=$\frac{PC}{PC′}$,求证:平面ABC∥平面A′B′C′.
如图,从平面ABC外一点P,引射线PA、PB、PC,在它们上面分别取点A′、B′、C′,使$\frac{PA}{PA′}$=$\frac{PB}{PB′}$=$\frac{PC}{PC′}$,求证:平面ABC∥平面A′B′C′.