题目内容
6.把半径为R的金属球切削成圆柱形的零件,要使车下来的金属屑最少,那么这个圆柱形零件的高应为多少?分析 由题意,就是求这个圆柱形零件的最大体积.设圆柱的高为h,可得圆柱的底面半径,求出体积,利用导数求解即可.
解答 解:由题意,就是求这个圆柱形零件的最大体积.
设圆柱的高为h,则圆柱的底面半径为r=$\sqrt{{R}^{2}-\frac{{h}^{2}}{4}}$,
∴圆柱的体积V=πr2h=π(R2-$\frac{{h}^{2}}{4}$)h(0≤h≤R)V′=πR2-$\frac{3π}{4}$πh2=0,可得h=$\frac{2\sqrt{3}}{3}$R,
函数在(0,$\frac{2\sqrt{3}}{3}$R)上单调递增,在($\frac{2\sqrt{3}}{3}$R,+∞)上单调递减,
∴h=$\frac{2\sqrt{3}}{3}$R时,V最大$\frac{4\sqrt{3}}{9}π{R}^{3}$.
点评 本题考查圆柱的体积,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.设f(x)=a${\;}^{x-\frac{1}{2}}$(a>0,且a≠1),满足f(lga)=$\sqrt{10}$,则a的取值范围是( )
| A. | {1,0} | B. | {5,$\frac{\sqrt{10}}{10}$} | C. | {10,$\frac{\sqrt{10}}{10}$} | D. | {10,$\frac{\sqrt{10}}{5}$} |
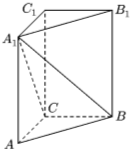 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,三棱锥A1-ABC的体积为$\frac{8}{3}$,求直线A1B与CC1所成角的大小(结果用反三角函数值表示).
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,三棱锥A1-ABC的体积为$\frac{8}{3}$,求直线A1B与CC1所成角的大小(结果用反三角函数值表示).