题目内容
设函数f(x)的导函数为f′(x),若f(x)=ax3-ax2+[| f′(1) | 2 |
(1)a表示f′(1);
(II)若函数f(x)f在R上存在极值,求a的范围.
分析:(1)因为f′(1)为常数,故将f(x)求导,令x=1,即可用a表示f′(1);
(2)若函数f(x)f在R上存在极值,则f′(x)=0必须有两个相异根,故△>0,解不等式即可.
(2)若函数f(x)f在R上存在极值,则f′(x)=0必须有两个相异根,故△>0,解不等式即可.
解答:解:(I)f′(x)=3ax2-2ax+
-1,
把x=1代入上式得f′(1)=a+
-1,
所以f′(1)=2a-2;
(II)由(1)可知:f′(x)=3ax2-2ax+a-2,
a=0时,f′(x)=-2<0,所以f(x)在R上单调递减,无极值;
当a≠0时,若函数f(x)f在R上存在极值,则f′(x)=0必须有两个相异根.
故△>0,即4a2-4×3a×(a-2)>0,
即4a2-12a(a-2)>0,
解得0<a<3.
| f′(1) |
| 2 |
把x=1代入上式得f′(1)=a+
| f′(1) |
| 2 |
所以f′(1)=2a-2;
(II)由(1)可知:f′(x)=3ax2-2ax+a-2,
a=0时,f′(x)=-2<0,所以f(x)在R上单调递减,无极值;
当a≠0时,若函数f(x)f在R上存在极值,则f′(x)=0必须有两个相异根.
故△>0,即4a2-4×3a×(a-2)>0,
即4a2-12a(a-2)>0,
解得0<a<3.
点评:本题考查求函数的导数、对导数的认识,及函数存在极值的条件等知识,难度不大.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
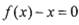 有实数根;
有实数根;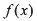 的导数
的导数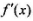 (满足
(满足 ”
” 为集合M中的任一元素,试证明万程
为集合M中的任一元素,试证明万程 只有一个实根;
只有一个实根;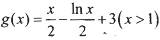 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;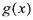 定义域内的任一区间
定义域内的任一区间 ,都存在
,都存在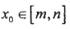 ,使得
,使得 ”,请利用函数
”,请利用函数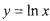 的图象说明这一结论.
的图象说明这一结论.