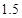题目内容
对于函数 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为“和谐函数”,区间
为“和谐函数”,区间 为函数
为函数 的一个“和谐区间”.给出下列4个函数:
的一个“和谐区间”.给出下列4个函数:
①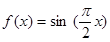 ;②
;② ;③
;③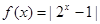 ; ④
; ④ .
.
其中存在唯一“和谐区间”的“和谐函数”为 ( )
| A.①②③ | B.②③④ | C.①③ | D.②③ |
D
解析试题分析:对于①,由于函数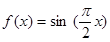 的周期是4,正弦函数的性质我们易得,A=[0,1]为函数的一个“和谐区间”;同时当A=[-1,0]时也是函数的一个“和谐区间”,∴不满足唯一性;
的周期是4,正弦函数的性质我们易得,A=[0,1]为函数的一个“和谐区间”;同时当A=[-1,0]时也是函数的一个“和谐区间”,∴不满足唯一性;
对于②,由于 =2x2-1,当A=[-1,1]时,
=2x2-1,当A=[-1,1]时, ∈[-1,1],满足条件,且由二次函数的图象可知,满足条件的集合只有A=[-1,1]一个.∴
∈[-1,1],满足条件,且由二次函数的图象可知,满足条件的集合只有A=[-1,1]一个.∴ =2x2-1满足题意;
=2x2-1满足题意;
对于③,由指数函数的性质我们易得,M=[0,1]为函数 =|2x-1|的“和谐区间”,由指数函数的图象可和,满足条件的集合只有A=[0,1]一个.∴
=|2x-1|的“和谐区间”,由指数函数的图象可和,满足条件的集合只有A=[0,1]一个.∴ =|2x-1|满足题意;
=|2x-1|满足题意;
对于④,由于 =ln(x+1)单调递增,且函数的定义域为(-1,+∞),若存在“和谐区间”,则满足
=ln(x+1)单调递增,且函数的定义域为(-1,+∞),若存在“和谐区间”,则满足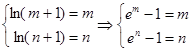 ,∴m,n是方程
,∴m,n是方程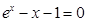 的两个根,设
的两个根,设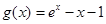 ,
,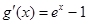 ,当x>0时,
,当x>0时,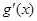 >0,此时函数
>0,此时函数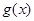 单调递增,当-1<x<0时,
单调递增,当-1<x<0时,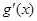 <0,此时函数
<0,此时函数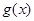 单调递减,且
单调递减,且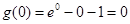 ,故
,故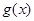 =ex-x-1=0有且只有一个解,故
=ex-x-1=0有且只有一个解,故 =ln(x+1)不存在“可等域区间”.故存在唯一“和谐区间”的“和谐函数”为:②③.故选:D.
=ln(x+1)不存在“可等域区间”.故存在唯一“和谐区间”的“和谐函数”为:②③.故选:D.
考点:1.函数的概念;2.函数的图象与性质;3.新定义.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案定义在R上的函数 具有下列性质:①
具有下列性质:① ;②
;② ;③
;③ 在
在 上为增函数,则对于下述命题:
上为增函数,则对于下述命题:
① 为周期函数且最小正周期为4;
为周期函数且最小正周期为4;
② 的图像关于
的图像关于 轴对称且对称轴只有1条;
轴对称且对称轴只有1条;
③ 在
在 上为减函数.
上为减函数.
正确命题的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
方程 实根的个数为( )
实根的个数为( )
| A.6 | B.5 | C.4 | D.3 |
函数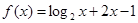 的零点必落在区间( )
的零点必落在区间( )
A.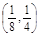 | B.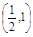 | C.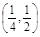 | D.(1,2) |
已知函数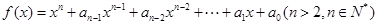 ,设
,设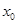 是函数
是函数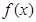 的零点的最大值,则下列论断一定错误的是( )
的零点的最大值,则下列论断一定错误的是( )
A.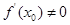 | B.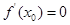 | C.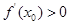 | D.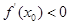 |
下列函数中,满足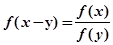 的单调递减函数是( )
的单调递减函数是( )
A.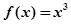 | B.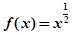 | C.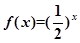 | D.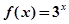 |
函数 的单调递增区间是( )
的单调递增区间是( )
A. | B. | C. | D. |
对任意实数 ,记
,记 ,若
,若 ,其中奇函数
,其中奇函数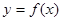 在
在 时有极小值
时有极小值 ,
, 是正比例函数,
是正比例函数, 与
与 图象如图,则下列关于
图象如图,则下列关于 的说法中正确的是( )
的说法中正确的是( )
A. 是奇函数 是奇函数 |
B. 有极大值 有极大值 和极小值 和极小值 |
C. 的最小值为 的最小值为 ,最大值为2 ,最大值为2 |
D. 在 在 上是增函数 上是增函数 |
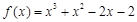 的一个正数零点附近的函数值用二分法计算,得数据如下:
的一个正数零点附近的函数值用二分法计算,得数据如下: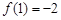
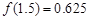
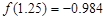
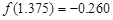

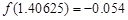
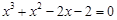 的一个最接近的近似根为( )
的一个最接近的近似根为( )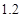 B.
B.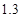 C.
C.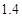 D.
D.