题目内容
我们知道,直线与圆的位置关系可以用圆心到直线的距离进行判别,那么直线与椭圆的位置关系有类似的判别方法吗?请同学们进行研究并完成下面的问题.(1)设F1、F2是椭圆M:
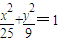 的两个焦点,点F1、F2到直线l:
的两个焦点,点F1、F2到直线l: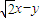
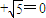 的距离分别为d1、d2,试求d1•d2的值,并判断直线l与椭圆M的位置关系.
的距离分别为d1、d2,试求d1•d2的值,并判断直线l与椭圆M的位置关系.(2)设F1、F2是椭圆M:
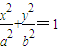 (a>b>0)的两个焦点,点F1、F2到直线l:mx+ny+p=0(m、n不同时为零)的距离分别为d1、d2,且直线l与椭圆M相切,试求d1•d2的值.
(a>b>0)的两个焦点,点F1、F2到直线l:mx+ny+p=0(m、n不同时为零)的距离分别为d1、d2,且直线l与椭圆M相切,试求d1•d2的值.(3)试写出一个能判断直线与椭圆的相交、相离位置关系的充要条件(不必证明).
【答案】分析:(1)利用点到直线的距离公式分别计算d1、d2,代入d1•d2化简,可以求出d1•d2的值,再通过直线L与椭圆方程消去y得到关于x的方程,可以求出根的差别式大于零,得到直线L与椭圆M有两个交点,是相交的位置关系;
(2)将直线方程与椭圆方程消去y,得到关于x的方程.再利用根的判别式可得△=0,从而p2=a2m2+b2n2,将其代入d1•d2的表达式化简可得d1•d2=b2;
(3)根据(2)运算得启发:直线L与椭圆M相交的充要条件为:d1d2<b2;直线L与椭圆M相离的充要条件为:d1d2>b2.
解答:解:(1)∵F1(-4,0),F2(4,0)到直线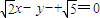 的距离分别为
的距离分别为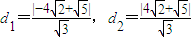
∴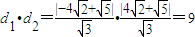
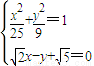
∴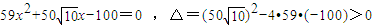
∴直线l与椭圆C相交
(2)F1(-c,0),F2(c,0),直线l与椭圆M相切,点F1、F2在直线l的同侧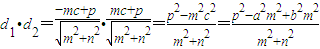
又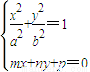
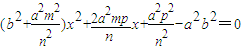
∴△=0
∴p2=b2n2+a2m2
∴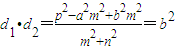
(3)设F1、F2是椭圆M: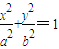 (a>b>0)的两个焦点,点F1、F2到直线l:mx+ny+p=0(m、n不同时为零)的距离分别为d1、d2,且点F1、F2在直线l的同侧,那么,直线l与椭圆M相交的充要条件为:d1•d2<b2;直线l与椭圆M相离的充要条件为:d1•d2>b2;
(a>b>0)的两个焦点,点F1、F2到直线l:mx+ny+p=0(m、n不同时为零)的距离分别为d1、d2,且点F1、F2在直线l的同侧,那么,直线l与椭圆M相交的充要条件为:d1•d2<b2;直线l与椭圆M相离的充要条件为:d1•d2>b2;
点评:本题考查了直线与圆锥曲线的位置关系、类比推理以及圆锥曲线的综合应用等知识点,属于难题.本题对运算的要求相当高,解题中应注意设而不求和转化化归思想的运用.
(2)将直线方程与椭圆方程消去y,得到关于x的方程.再利用根的判别式可得△=0,从而p2=a2m2+b2n2,将其代入d1•d2的表达式化简可得d1•d2=b2;
(3)根据(2)运算得启发:直线L与椭圆M相交的充要条件为:d1d2<b2;直线L与椭圆M相离的充要条件为:d1d2>b2.
解答:解:(1)∵F1(-4,0),F2(4,0)到直线
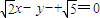 的距离分别为
的距离分别为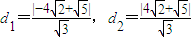
∴
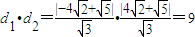
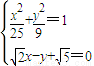
∴
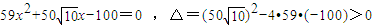
∴直线l与椭圆C相交
(2)F1(-c,0),F2(c,0),直线l与椭圆M相切,点F1、F2在直线l的同侧
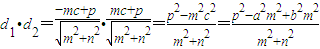
又
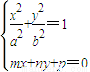
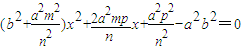
∴△=0
∴p2=b2n2+a2m2
∴
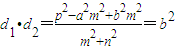
(3)设F1、F2是椭圆M:
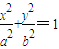 (a>b>0)的两个焦点,点F1、F2到直线l:mx+ny+p=0(m、n不同时为零)的距离分别为d1、d2,且点F1、F2在直线l的同侧,那么,直线l与椭圆M相交的充要条件为:d1•d2<b2;直线l与椭圆M相离的充要条件为:d1•d2>b2;
(a>b>0)的两个焦点,点F1、F2到直线l:mx+ny+p=0(m、n不同时为零)的距离分别为d1、d2,且点F1、F2在直线l的同侧,那么,直线l与椭圆M相交的充要条件为:d1•d2<b2;直线l与椭圆M相离的充要条件为:d1•d2>b2;点评:本题考查了直线与圆锥曲线的位置关系、类比推理以及圆锥曲线的综合应用等知识点,属于难题.本题对运算的要求相当高,解题中应注意设而不求和转化化归思想的运用.

练习册系列答案
相关题目
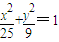 的两个焦点,点F1、F2到直线l:
的两个焦点,点F1、F2到直线l: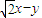
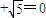 的距离分别为d1、d2,试求d1•d2的值,并判断直线l与椭圆M的位置关系.
的距离分别为d1、d2,试求d1•d2的值,并判断直线l与椭圆M的位置关系.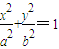 (a>b>0)的两个焦点,点F1、F2到直线l:mx+ny+p=0(m、n不同时为零)的距离分别为d1、d2,且直线l与椭圆M相切,试求d1•d2的值.
(a>b>0)的两个焦点,点F1、F2到直线l:mx+ny+p=0(m、n不同时为零)的距离分别为d1、d2,且直线l与椭圆M相切,试求d1•d2的值.