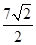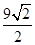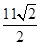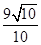题目内容
已知函数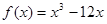 ,若
,若 在区间
在区间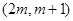 上单调递减,则实数
上单调递减,则实数 的取值范围是( )
的取值范围是( )
A. | B.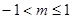 | C.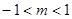 | D.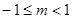 |
D
解析试题分析: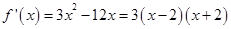 ,知函数在
,知函数在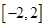 上单调递减,若
上单调递减,若 在区间
在区间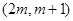 上单调递减,可得
上单调递减,可得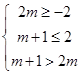 ,解得
,解得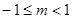 .
.
考点:导数与函数的单调性.

练习册系列答案
相关题目
已知函数 的导函数为
的导函数为 ,若
,若 时,
时, ;
; ;
; 时,
时, ,则
,则 ( )
( )
| A.25 | B.17 | C. | D.1 |
已知 在R上开导,且
在R上开导,且 ,若
,若 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
定积分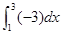 等于( )
等于( )
A.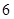 | B.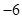 | C.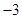 | D.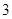 |
若函数 在R上可导,且
在R上可导,且 ,则( )
,则( )
A. | B. | C. | D.无法确定 |
由直线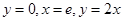 及曲线
及曲线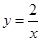 所围成的封闭的图形的面积为( )
所围成的封闭的图形的面积为( )
A.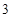 | B.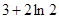 | C.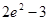 | D.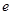 |
函数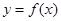 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )
A.若函数在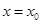 时取得极值,则 时取得极值,则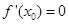 |
B.若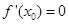 ,则函数在 ,则函数在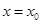 处取得极值 处取得极值 |
C.若在定义域内恒有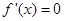 ,则 ,则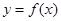 是常数函数 是常数函数 |
D.函数 在 在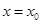 处的导数是一个常数 处的导数是一个常数 |
设f(x)=- x3+
x3+ x2+2ax,若f(x)在(
x2+2ax,若f(x)在( ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )
A.a>- | B.a<- | C.a> | D.不存在 |
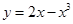 在横坐标为
在横坐标为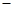 l的点处的切线为
l的点处的切线为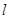 ,则点P(3,2)到直线
,则点P(3,2)到直线