题目内容
已知三条直线L1:x-2y=0L2:y+1=0L3:2x+y-1=0两两相交,先画出图形,再求过这三个交点的圆的方程.
分析:先根据题意画出三条直线,再判断由三个交点构成的三角形的形状为直角三角形,并有直线联立求得顶点坐标,最后求出圆心坐标和半径,写出圆的标准方程即可
解答: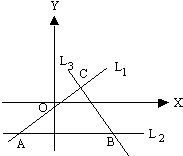 解:如图:通过计算斜率可得L1⊥L3,经过A,B,C三点的圆就是以AB为直径的圆
解:如图:通过计算斜率可得L1⊥L3,经过A,B,C三点的圆就是以AB为直径的圆
解方程组
得
所以点A的坐标(-2,-1)
解方程组
得
所以点B的坐标(1,-1)
线段AB的中点坐标是(-
,-1),
又|AB|=
=3
所以圆的方程是(x+
)2+(y+1)2=
 解:如图:通过计算斜率可得L1⊥L3,经过A,B,C三点的圆就是以AB为直径的圆
解:如图:通过计算斜率可得L1⊥L3,经过A,B,C三点的圆就是以AB为直径的圆解方程组
|
得
|
所以点A的坐标(-2,-1)
解方程组
|
得
|
所以点B的坐标(1,-1)
线段AB的中点坐标是(-
| 1 |
| 2 |
又|AB|=
| (-2-1)2+(-1+1)2 |
所以圆的方程是(x+
| 1 |
| 2 |
| 9 |
| 4 |
点评:本题考察了直线方程即画法,求直线交点的方法,求圆的标准方程的方法,准确的判断三角形的形状是解决本题的关键

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目