题目内容
将5名同学分到甲、乙、丙3个小组,若甲组至少两人,乙、丙组至少各一人,则不同的分配方案的种数为( )
| A.80 | B.120 | C.140 | D.180 |
A
解析试题分析:分两类:若甲组两人,则乙、丙两组的方法数是 ,此时的方法种数为
,此时的方法种数为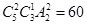 ;若甲组3人,则方法数
;若甲组3人,则方法数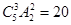 ,根据分类加法原理得总的方法总数为60+20=80,故选A
,根据分类加法原理得总的方法总数为60+20=80,故选A
考点:本题考查了排列组合的综合运用
点评:熟练掌握排列、组合的综合运用是解决此类问题的关键,属基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
由数字0,1,2,3,4,5组成的奇偶数字相间且无重复数字的六位数的个数是
| A.36 | B.48 | C.60 | D.72 |
乘积 等于( )
等于( )
A. | B. | C. | D. |
高二某同学有A、B两类不同的校庆明信片,其中A类明信片2张,B类明信片3张,他想从中取出4张寄给初中的4位老师,每位老师1张,则不同的选择方法有( )
| A.4种 | B.10种 | C.18种 | D.20种 |
现有四件不同款式的上衣与三件不同颜色的长裤,如果一条长裤与一件上衣配成一套,则不同的选法数为
| A.7 | B.64 | C.12 | D.81 |
设 为奇数,那么
为奇数,那么 除以13的余数是( )
除以13的余数是( )
A. | B. | C.  | D. |
在二项式(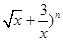 的展开式中,各项系数之和为M,各项二项式系数之和为N,且M+N=72,则展开式中常数项的值为
的展开式中,各项系数之和为M,各项二项式系数之和为N,且M+N=72,则展开式中常数项的值为
| A.18 | B.12 | C.9 | D.6 |
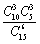

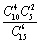
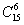

 ,则质点P移动六次后位于点(4,2)的概率是 ( )
,则质点P移动六次后位于点(4,2)的概率是 ( )


