题目内容
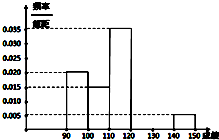 某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.(Ⅰ)请补充完整频率分布直方图,并估计这组数据的平均数M;(Ⅱ)若不低于120分的同学进入决赛,不低于140分的同学为种子选手,完成下面2×2列联表(即填写空格处的数据).
| [120,140) | [140,150] | 合计 | |
| 参加培训 | 5 | 8 | |
| 未参加培训 | |||
| 合计 | 4 |
分析:(Ⅰ)设第四,五组的频率分别为x,y,则2y=x+0.005×10,x+y=1-(0.005+0.015+0.02+0.035)×10,解得x=0.15,y=0.10,从而得出直方图和平均数M;
(Ⅱ)先求出进入决赛的人数,然后根据2×2列联表中的数据可求出空格处的数据,从而完成2×2列联表.
(Ⅱ)先求出进入决赛的人数,然后根据2×2列联表中的数据可求出空格处的数据,从而完成2×2列联表.
解答:解:(Ⅰ)设第四,五组的频率分别为x,y,则2y=x+0.005×10①
x+y=1-(0.005+0.015+0.02+0.035)×10②
由①②解得x=0.15,y=0.10(2分)
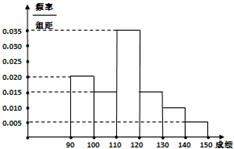
从而得出直方图(如图所示)
 (4分)
(4分)
M=95×0.2+105×0.15+115×0.35+125×0.15+135×0.1+145×0.05=114.5(6分)
(Ⅱ)依题意,进入决赛人数为
×(0.15+0.10+0.05)=24,进而填写列联表如下:
…(12分)
x+y=1-(0.005+0.015+0.02+0.035)×10②
由①②解得x=0.15,y=0.10(2分)
从而得出直方图(如图所示)
 (4分)
(4分)M=95×0.2+105×0.15+115×0.35+125×0.15+135×0.1+145×0.05=114.5(6分)
(Ⅱ)依题意,进入决赛人数为
| 4 |
| 0.05 |
| [120,140) | [140,150] | 合计 | |
| 参加培训 | 5 | 3 | 8 |
| 未参加培训 | 15 | 1 | 16 |
| 合计 | 20 | 4 | 24 |
点评:本题主要考查了频率分布直方图,以及2×2列联表的填写,同时考查了分析问题的能力,属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].图(1)为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)请补充完整频率分布直方图,并估计这组数据的平均数M;
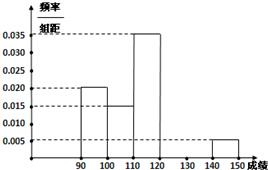
(Ⅱ)若不低于120分的同学进入决赛,不低于140分的同学为种子选手,完成下面2×2
列联表(即填写空格处的数据),并判断是否有99%的把握认为“进入决赛的同学
成为种子选手与专家培训有关”.
附:K2=
(Ⅰ)请补充完整频率分布直方图,并估计这组数据的平均数M;

(Ⅱ)若不低于120分的同学进入决赛,不低于140分的同学为种子选手,完成下面2×2
列联表(即填写空格处的数据),并判断是否有99%的把握认为“进入决赛的同学
成为种子选手与专家培训有关”.
a≥-
|
[140,150] | 合计 | |||
| 参加培训 | 5 | 8 | |||
| 未参加培训 | |||||
| 合计 | 4 |
附:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
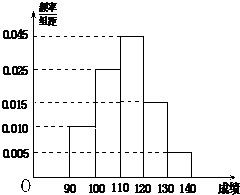 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.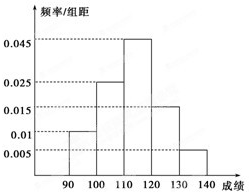 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为2人. 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.