题目内容
已知实数x、y 仅满足x•y>0,且
+
+
=1,则xy取值的范围是( )
| 8 |
| xy |
| 1 |
| x |
| 1 |
| y |
分析:将
+
+
=1变形为x+y=xy-8,再结合已知条件,利用基本不等式即可.
| 8 |
| xy |
| 1 |
| x |
| 1 |
| y |
解答:解:∵
+
+
=1,
∴
=1-
-
=
,
∴xy=8+(x+y),
∴x+y=8-xy,
又x•y>0,
∴若x>0,y>0,则
>0,
∴8-xy=x+y≥2
(当且仅当x=y时取等号),
∴(
+4)(
-2)≤0,
∴-4≤
≤2,又
>0,
∴0<
≤2,
∴0<xy≤4;
若x<0,y<0,-x>0,-y>0,
同理可得8-xy≤-2
,
∴
≥4或
≤-2(舍去),
∴xy≥16.
综上所述,0<xy≤4或xy≥16.
故选D.
| 8 |
| xy |
| 1 |
| x |
| 1 |
| y |
∴
| 8 |
| xy |
| 1 |
| x |
| 1 |
| y |
=
| xy-(x+y) |
| xy |
∴xy=8+(x+y),
∴x+y=8-xy,
又x•y>0,
∴若x>0,y>0,则
| xy |
∴8-xy=x+y≥2
| xy |
∴(
| xy |
| xy |
∴-4≤
| xy |
| xy |
∴0<
| xy |
∴0<xy≤4;
若x<0,y<0,-x>0,-y>0,
同理可得8-xy≤-2
| xy |
∴
| xy |
| xy |
∴xy≥16.
综上所述,0<xy≤4或xy≥16.
故选D.
点评:本题考查基本不等式的应用,考查转化思想与分类讨论思想及对等式变形应用的能力,属于中档题.

练习册系列答案
相关题目
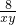 +
+ +
+ =1,则xy取值的范围是
=1,则xy取值的范围是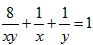 ,则xy取值的范围是
,则xy取值的范围是