题目内容
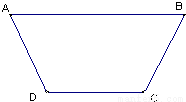
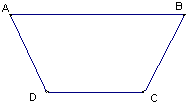 国家加大水利工程建设,某地区要修建一条灌溉水渠,其横断面为等腰梯形(如图),底角A为600,考虑到坚固性及用料原因,要求其横断面的面积为6
国家加大水利工程建设,某地区要修建一条灌溉水渠,其横断面为等腰梯形(如图),底角A为600,考虑到坚固性及用料原因,要求其横断面的面积为6| 3 |
(1).求y关于x的函数关系式,并指出其定义域;
(2).当水渠的腰长x为多少米时,水泥用料最省(即断面的用料部分的周长最小)?求此时用料周长的值
(3).如果水渠的深限制在[3,
| 3 |
分析:(1)求y关于x的函数关系式,关键是求渠底BC及两腰的长;
(2)先利用解直角三角形知识求横截面的周长,再结合基本不等式求出周长面积的最小值即可;
(3)先利用函数单调性的定义探求(2)中周长函数的单调性,再结合所给自变量的范围即可求横截面周长的最小值.
(2)先利用解直角三角形知识求横截面的周长,再结合基本不等式求出周长面积的最小值即可;
(3)先利用函数单调性的定义探求(2)中周长函数的单调性,再结合所给自变量的范围即可求横截面周长的最小值.
解答:解:(1)由AD=BC+2
,及S=
(AD+BC)x=6
,
得BC=
-
,又
,得0<x<3
,-----------------------(4分)
所以y=BC+2AB=
+
x,定义域为(0,3
)------------------------(6分)
(2)y=
+
x≥2
=6
,当且仅当,即x=
∈(0,12)时等号成立,
所以用料周长最少为6
米,此时腰长为
米.----------------------(10分)
(3)x∈[3,2
],y=
(x+
)递增,所以x=3时,ymin=5
米-------------------------(15分)
| x | ||
|
| 1 |
| 2 |
| 3 |
得BC=
6
| ||
| x |
| x | ||
|
|
| 2 |
所以y=BC+2AB=
6
| ||
| x |
| 3 |
| 2 |
(2)y=
6
| ||
| x |
| 3 |
|
| 2 |
| 6 |
所以用料周长最少为6
| 2 |
| 6 |
(3)x∈[3,2
| 3 |
| 3 |
| 6 |
| x |
| 3 |
点评:本题主要考查了基本不等式在最值问题中的应用、函数在实际问题中的应用等知识,对于(3)问应主要利用函数的单调性求解,属于中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 ,考虑到坚固性及用料,要求横断面的面
,考虑到坚固性及用料,要求横断面的面 积为
积为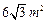 ,记水渠深为x m,用料部分的周长(即渠底BC及两腰长的和)为y
,记水渠深为x m,用料部分的周长(即渠底BC及两腰长的和)为y m。
m。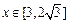 时,横断面用料部分的周长最小?最小值是多少米?
时,横断面用料部分的周长最小?最小值是多少米?
 ,考虑到坚固性及用料,要求横断面的面积为
,考虑到坚固性及用料,要求横断面的面积为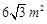 ,记水渠深为x m,用料部分的周长(即渠底BC及两腰长的和)为y m。
,记水渠深为x m,用料部分的周长(即渠底BC及两腰长的和)为y m。 时,横断面用料部分的周长最小?最小值是多少米?
时,横断面用料部分的周长最小?最小值是多少米?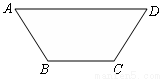
 国家加大水利工程建设,某地区要修建一条灌溉水渠,其横断面为等腰梯形(如图),底角
国家加大水利工程建设,某地区要修建一条灌溉水渠,其横断面为等腰梯形(如图),底角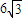 平方米,记水渠深为x米,用料部分的周长(即渠底BC及两腰长的和)为y米,
平方米,记水渠深为x米,用料部分的周长(即渠底BC及两腰长的和)为y米,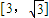 范围内时,横断面用料部分周长的最小值是多少米?
范围内时,横断面用料部分周长的最小值是多少米?