题目内容
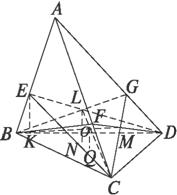
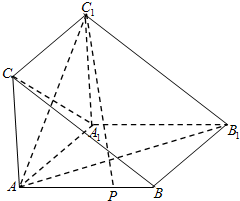
如图，在体积为1的三棱锥A—BCD侧棱AB、AC、AD上分别取点E、F、G， 使AE : EB=AF : FC=AG : GD=2 : 1，记O为三平面BCG、CDE、DBF的交点，则三棱锥O—BCD的体积等于 （ ）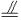
A．
B．
C． 
D．
C
解析：如下图所示：
MC为△ECD与△GBC交线，ND为△FBD与△ECD交线.
∴O点必为MC与ND交点.
∵==
，
∴E到△BCD距离h1为三棱锥A—BCD的高h的
，即h1=
h.
又∵EF
BC，
∴
=
.
∴N到△BCD距离h2=
h1=
×
h=
h.
∵MN
CD，
∴
=
.
∴O到△BCD距离h3=
h2=
×
h=
h.
∴三棱锥O—BCD的高为h3=
h.
∴VO—BCD=
S△BCD·
h
=
×（
S△BCD·h）
=
×VA—BCD
=
×1
=
.
练习册系列答案
星级口算天天练系列答案
相关题目
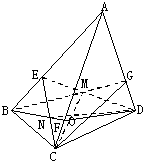
如图，在体积为1的三棱锥A-BCD侧棱AB、AC、AD上分别取点E、F、G，使AE：EB=AF：FC=AG：GD=2：1，记O为三平面BCG、CDE、DBF的交点，则三棱锥O-BCD的体积等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在体积为1的三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AC⊥AB，AC=AA1=1，P为线段AB上的动点．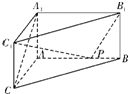
（2012•蓝山县模拟）如图，在体积为1的三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥AC，AC=AA1=1，P为线段AB上的动点．
B
C.
D.
