题目内容
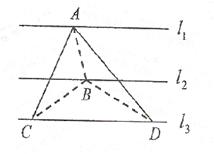
不共面的三条定直线l1，l2，l3互相平行，点A在l1上，点B在l2上，C、D两点在l3上，若CD=a（定值），则三棱锥A-BCD的体积（ ）
分析：通过三条平行直线是固定的，推出三角形的面积固定，三棱锥顶点到底面的距离是固定的，说明棱锥的体积是定值即可．
解答：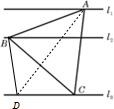
解：因为三条平行线是固定的，所以B到CD的距离是定值，所以三角形BCD的面积是定值，A到三角形BCD的距离也是定值，所以三棱锥A-BCD的体积V=
S△BCD•hA=定值．
故选D．
解：因为三条平行线是固定的，所以B到CD的距离是定值，所以三角形BCD的面积是定值，A到三角形BCD的距离也是定值，所以三棱锥A-BCD的体积V=| 1 |
| 3 |
故选D．
点评：本题考查棱锥的体积的求法，同底等高体积相等，考查基本知识的应用．
练习册系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
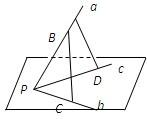9、已知不共面的三条直线a、b、c相交于点P，A∈a，B∈a，C∈b，D∈c，求证：AD与BC是异面直线．
相互平行，点
在
上，点
在
上，
两点在
上，若
（定值），则三棱锥
的体积（ ）
，
，
互相平行，点A在
（定值），则三棱锥A－BCD的体积（ ）.