Question

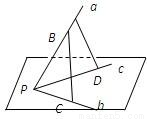
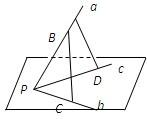9、已知不共面的三条直线a、b、c相交于点P，A∈a，B∈a，C∈b，D∈c，求证：AD与BC是异面直线．

Answer 1

分析：可以用反证法，假设AD和BC共面，推出直线a、b、c都在同一个平面内，矛盾；还可以利用经过平面内一点与平面外一点的直线，和平面内不经过此点的直线是异面直线．

解答：证明：法一：（反证法）假设AD和BC共面，所确定的平面为α，
那么点P、A、B、C、D都在平面α内，
∴直线a、b、c都在平面α内，与已知条件a、b、c不共面矛盾，
假设不成立，∴AD和BC是异面直线．
法二：（直接证法）∵a∩c=P，∴它们确定一个平面，
设为α，由已知C∉平面α，B∈平面α，
AD?平面α，B∉AD，
∴AD和BC是异面直线．

点评：本题考查异面直线的证明方法，反证法或用判定定理．