题目内容
(A题) (奥赛班做)有三个信号监测中心A、B、C,A位于B的正东方向,相距6千米,C在B的北偏西30°,相距4千米.在A测得一信号,4秒后,B、C才同时测得同一信号,试建立适当的坐标系,确定信号源P的位置(即求出P点的坐标).(设该信号的传播速度为1千米/秒,图见答卷)
分析:由于B、C同时发现信号,则P在线段BC的中垂线上,又由A、B两舰发现信号的时间差为4秒,知|PB|-|PA|=4,从而P在双曲线的右支上,所以可确定P的坐标,从而问题得解.
解答: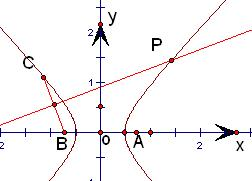 解:取A、B所在直线为x轴,线段AB的中点O为原点,
解:取A、B所在直线为x轴,线段AB的中点O为原点,
建立直角坐标系.则A、B、C的坐标为
A( 3,0 )、B (-3,0 )、C (-5,2
),(长度单位为千米).
由已知|PB|-|PA|=4,所以点P在以A、B为焦点,
实轴长为4的双曲线的右支上,
其方程为
-
=1(x≥2)①
又B、C同时测得同一信号,即有|PB|=|PC|
∴点P又在线段BC的中垂线上,
其方程为y-
=
(x+4),
即 y=
(x+7)②
由①、②解得:
,
∴得点P的坐标为 ( 8,5
).
 解:取A、B所在直线为x轴,线段AB的中点O为原点,
解:取A、B所在直线为x轴,线段AB的中点O为原点,建立直角坐标系.则A、B、C的坐标为
A( 3,0 )、B (-3,0 )、C (-5,2
| 3 |
由已知|PB|-|PA|=4,所以点P在以A、B为焦点,
实轴长为4的双曲线的右支上,
其方程为
| x2 |
| 4 |
| y2 |
| 5 |
又B、C同时测得同一信号,即有|PB|=|PC|
∴点P又在线段BC的中垂线上,
其方程为y-
| 3 |
| ||
| 3 |
即 y=
| ||
| 3 |
由①、②解得:
|
∴得点P的坐标为 ( 8,5
| 3 |
点评:本题主要考查从实际问题中构建数学模型,考查双曲线的定义、轨迹方程的求解,考查学生利用数学知识解决实际问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目