题目内容
设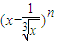 的展开式的各项系数之和为M,二项式系数之和为N,若M+N=16,则展开式中的常数项为 .
的展开式的各项系数之和为M,二项式系数之和为N,若M+N=16,则展开式中的常数项为 .
【答案】分析:根据题意,在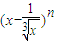 中令x=1可得M,由二项式系数的性质可得N,又由题意M+N=16可得2n=16,解可得n的值,再根据二项式定理可得(x-
中令x=1可得M,由二项式系数的性质可得N,又由题意M+N=16可得2n=16,解可得n的值,再根据二项式定理可得(x-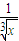 )4的展开式的通项,令x的系数为0可得r的值,将r的值代入可得通项可得其常数项,即可得答案.
)4的展开式的通项,令x的系数为0可得r的值,将r的值代入可得通项可得其常数项,即可得答案.
解答:解:根据题意,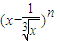 的展开式的各项系数之和为M,
的展开式的各项系数之和为M,
在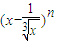 中令x=1可得,M=(1-1)n=0
中令x=1可得,M=(1-1)n=0
该展开式的二项式系数之和为N,则N=2n,
又由题意,M+N=16,则有2n=16,解可得n=4,
则(x-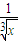 )4的展开式的通项为Tr+1=C4r(x)4-r•(-
)4的展开式的通项为Tr+1=C4r(x)4-r•(-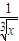 )r=(-1)r•C4r•
)r=(-1)r•C4r•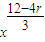 ,
,
令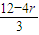 =0,可得r=3,
=0,可得r=3,
此时展开式中的常数项T4=(-1)3•C43=-4;
故答案为-4.
点评:本题考查二项式定理的应用,要注意展开式中“各项系数之和”与“二项式系数之和”的不同.
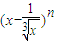 中令x=1可得M,由二项式系数的性质可得N,又由题意M+N=16可得2n=16,解可得n的值,再根据二项式定理可得(x-
中令x=1可得M,由二项式系数的性质可得N,又由题意M+N=16可得2n=16,解可得n的值,再根据二项式定理可得(x-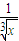 )4的展开式的通项,令x的系数为0可得r的值,将r的值代入可得通项可得其常数项,即可得答案.
)4的展开式的通项,令x的系数为0可得r的值,将r的值代入可得通项可得其常数项,即可得答案.解答:解:根据题意,
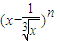 的展开式的各项系数之和为M,
的展开式的各项系数之和为M,在
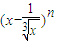 中令x=1可得,M=(1-1)n=0
中令x=1可得,M=(1-1)n=0该展开式的二项式系数之和为N,则N=2n,
又由题意,M+N=16,则有2n=16,解可得n=4,
则(x-
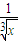 )4的展开式的通项为Tr+1=C4r(x)4-r•(-
)4的展开式的通项为Tr+1=C4r(x)4-r•(-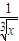 )r=(-1)r•C4r•
)r=(-1)r•C4r•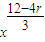 ,
,令
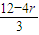 =0,可得r=3,
=0,可得r=3,此时展开式中的常数项T4=(-1)3•C43=-4;
故答案为-4.
点评:本题考查二项式定理的应用,要注意展开式中“各项系数之和”与“二项式系数之和”的不同.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 的展开式的各项系数之和为
的展开式的各项系数之和为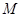 ,二项式系数之和为
,二项式系数之和为 ,若
,若 ,则展开式中常数项为___________.
,则展开式中常数项为___________. 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为(
)
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为(
) 的展开式的各项系数之和为M,二项式系数之和为N,若M,8,N三数成等比数列,则展开式中第四项为____
的展开式的各项系数之和为M,二项式系数之和为N,若M,8,N三数成等比数列,则展开式中第四项为____ 的展开式的各项系数之和为M,二项式系数之和为N,若
的展开式的各项系数之和为M,二项式系数之和为N,若 ,则展开式中
,则展开式中 的系数为 。
的系数为 。 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )