题目内容
有一批大小相同的呈正方体型的物件,按照上面少,下面多的方式,堆放于仓库的墙角处.从上至下,第一层放1件,第二层放3件,第三层放6件…,各层放置的平面图形如下: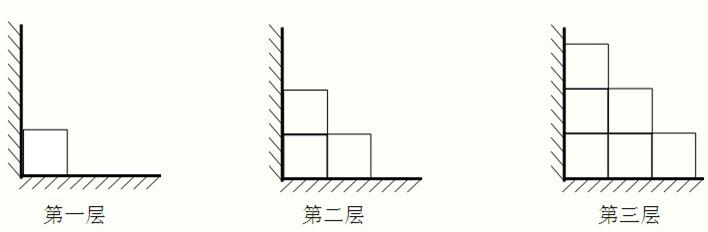
如果这堆物件一共堆放了10层,则第10层放有

如果这堆物件一共堆放了10层,则第10层放有
55
55
件这样的物件;这一堆共有220
220
件这样的物件.分析:设各层物件数构成数列{an},由题可知an-a n-1=n(n≥2)且a1=1.利用累加法求出通项公式an=
(n2+n),a10=可求.再利用分组求和法求和即可.
| 1 |
| 2 |
解答:解:设各层物件数构成数列{an},由题可知an-a n-1=n(n≥2)且a1=1.
所以a2-a1=2
a3-a2=3
…
an-a n-1=n (n≥2)
以上各式两边分别相加得
an-a1=2+3+…+n
∴an=1+2+3+…+n=
=
(n2+n)(n≥2),且a1=1也适合.
∴a10=55
S10=
(12+22+…+102)+
(1+2+…+10)
=
×
+
×
=220.
故答案为:55 220.
所以a2-a1=2
a3-a2=3
…
an-a n-1=n (n≥2)
以上各式两边分别相加得
an-a1=2+3+…+n
∴an=1+2+3+…+n=
| n(n+1) |
| 2 |
| 1 |
| 2 |
∴a10=55
S10=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 10×11×21 |
| 6 |
| 1 |
| 2 |
| 11×10 |
| 2 |
故答案为:55 220.
点评:本题考查数列求和,用到了累加法求通项,分组、公式法求和.考查建模解模的能力.公式12+22+32+…n2=
.
| n(n+1)(2n+1) |
| 6 |

练习册系列答案
相关题目